题目内容
将一颗质地均匀的正方体骰子(六个面的点数分别为1,2,3,4,5,6)先后抛掷两次,将得到的点数分别记为 .
.
(1)求直线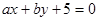 与圆
与圆 相切的概率;
相切的概率;
(2)将 的值分别作为三条线段的长,求这三条线段能围成等腰三角形的概率.
的值分别作为三条线段的长,求这三条线段能围成等腰三角形的概率.
(1)直线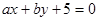 与圆
与圆 相切的概率为
相切的概率为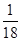 ;
;
(2)这三条线段能围成等腰三角形的概率为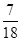 .
.
解析试题分析:(1)先后2次抛掷一枚骰子,将得到的点数分别记为 事件总数为36,直线
事件总数为36,直线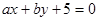 与圆
与圆 相切只有两种情况,所以相切的概率为
相切只有两种情况,所以相切的概率为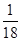 ;
;
(2)总事件共36种,这三条线段能围成等腰三角形有14种情况,故能围成等腰三角形的概率为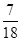 .
.
.
试题解析: (1)先后2次抛掷一枚骰子,将得到的点数分别记为 ,事件总数为6×6=36.
,事件总数为6×6=36.
因为直线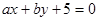 与圆
与圆 相切,所以有
相切,所以有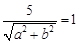 即:
即: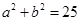 ,由于
,由于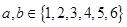
所以,满足条件的情况只有 或
或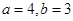 两种情况.
两种情况.
所以,直线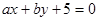 与圆
与圆 相切的概率是
相切的概率是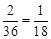
(2)先后2次抛掷一枚骰子,将得到的点数分别记为 ,事件总数为6×6=36.
,事件总数为6×6=36.
因为,三角形的一边长为5
所以,当 时,
时,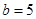 ,(1,5,5) 1种
,(1,5,5) 1种
当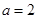 时,
时,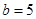 ,(2,5,5) 1种
,(2,5,5) 1种
当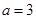 时,
时,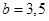 ,(3,3,5),(3,5,5) 2种
,(3,3,5),(3,5,5) 2种
当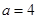 时,
时,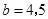 ,(4,4,5),(4,5,5) 2种
,(4,4,5),(4,5,5) 2种
当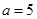 时,
时,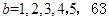 ,
,
(5,1,5),(5,2,5),(5,3,5),
(5,4,5),(5,5,5),(5,6,5) 6种
当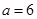 时,
时,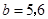 ,(6,5,5),(6,6,5) 2种
,(6,5,5),(6,6,5) 2种
故满足条件的不同情况共有14种.
所以,三条线段能围成不同的等腰三角形的概率为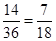 .
.
考点:古典概型、直线与圆的位置关系.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 ,每道程序中得优、良、中的概率分别为p1、
,每道程序中得优、良、中的概率分别为p1、 、p2.
、p2. 、
、 两个定点投篮位置,在
两个定点投篮位置,在 ,且在
,且在 位已经选拔入围的学生进行运动协调能力和逻辑思维能力的测试,其测试结果如下表:
位已经选拔入围的学生进行运动协调能力和逻辑思维能力的测试,其测试结果如下表:
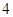 人.由于部分数据丢失,只知道从这
人.由于部分数据丢失,只知道从这 .
. ,
, 的值;
的值; 位,求其中至少有一位运动协调能力或逻辑思维能力优秀的学生的概率;
位,求其中至少有一位运动协调能力或逻辑思维能力优秀的学生的概率; ,求随机变量
,求随机变量 .
.
 表示空气质量达到一级的天数,求
表示空气质量达到一级的天数,求