题目内容
某选修课的考试按A级、B级依次进行,只有当A级成绩合格时,才可继续参加B级的考试.已知每级考试允许有一次补考机会,两个级别的成绩均合格方可获得该选修课的合格证书.现某人参加这个选修课的考试,他A级考试成绩合格的概率为 ,B级考试合格的概率为
,B级考试合格的概率为 .假设各级考试成绩合格与否均互不影响.
.假设各级考试成绩合格与否均互不影响.
(1)求他不需要补考就可获得该选修课的合格证书的概率;
(2)在这个考试过程中,假设他不放弃所有的考试机会,记他参加考试的次数为 ,求
,求 的数学期望E
的数学期望E .
.
(1) ,(2)
,(2)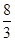 .
.
解析试题分析:(1)解概率问题,关键明确事件所包含的意义. 不需要补考就获得合格证书的事件为A级第一次考试合格且B级第一次考试合格,因为事件相互独立,所以由概率乘法得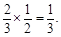 (2)参加考试的次数至少2次,至多4次,因此
(2)参加考试的次数至少2次,至多4次,因此 =2,3,4,因为不放弃所有的考试机会,所以
=2,3,4,因为不放弃所有的考试机会,所以 =2包含①A级第一次考试合格且B级第一次考试合格,②A级第一次考试不合格且A级补考不合格。
=2包含①A级第一次考试合格且B级第一次考试合格,②A级第一次考试不合格且A级补考不合格。 =4包含A级第一次考试不合格且A级补考合格, B级第一次考试不合格,B级补考合格或不合格.
=4包含A级第一次考试不合格且A级补考合格, B级第一次考试不合格,B级补考合格或不合格.  =3包含事件较多,可利用
=3包含事件较多,可利用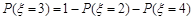 求解,最后再利用数学期望公式求E
求解,最后再利用数学期望公式求E .
.
试题解析:设“A级第一次考试合格”为事件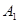 ,“A级补考合格”为事件A2; “B级第一次考试合格”为事件
,“A级补考合格”为事件A2; “B级第一次考试合格”为事件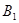 ,“B级补考合格”为事件
,“B级补考合格”为事件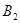 .
.
(1)不需要补考就获得合格证书的事件为A1·B1,注意到A1与B1相互独立,
则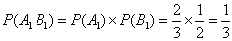
答:该考生不需要补考就获得合格证书的概率为 4
4
(2)由已知得, =2,3,4,注意到各事件之间的独立性与互斥性,可得
=2,3,4,注意到各事件之间的独立性与互斥性,可得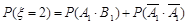
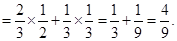 .6
.6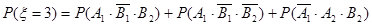
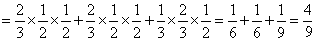 .8
.8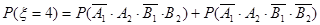
 .10
.10
故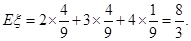
答:该考生参加考试次数的期望为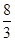 .13
.13
考点:古典概型概率,分布列及数学期望

练习册系列答案
 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案
相关题目
 ,每道程序中得优、良、中的概率分别为p1、
,每道程序中得优、良、中的概率分别为p1、 、p2.
、p2.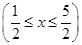 .
.