题目内容
已知
、
两个盒子中分别装有标记为
，
，
，
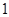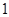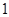的大小相同的四个小球，甲从盒中等可能地取出个球，乙从盒中等可能地取出个球．
（1）用有序数对
表示事件“甲抽到标号为
的小球，乙抽到标号为
的小球”，试写出所有可能的事件；
（2）甲、乙两人玩游戏，约定规则：若甲抽到的小球的标号比乙大，则甲胜；反之，则乙胜．你认为此规则是否公平？请说明理由．
（1）见解析（2）不公平，理由见解析
解析试题分析：（I）用列举法一一列举出甲、乙二人抽到的小球的所有情况，共16种不同情况．
（2）．甲抽到的小球的标号比乙大，有共6种情况；故甲胜的概率
，乙获胜的概率为
，故此游戏不公平．
试题解析：解：（I）甲、乙二人抽到的小球的所有情况为：
、
、
、
、
、
、
、
、
、
、
、
、
、
、
、
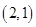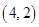，共16种不同情况． 6分
（2）甲抽到的小球的标号比乙大，有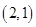、、、、、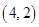，共6种情况， 8分
故甲胜的概率，乙获胜的概率为． 11分
因为
，所以此游戏不公平． 12分.
考点：古典概型及其概率计算公式.
练习册系列答案
教学练新同步练习系列答案
课前课后同步练习系列答案
相关题目
，每道程序中得优、良、中的概率分别为p1、
、p2.
、
两个定点投篮位置，在
，且在
位已经选拔入围的学生进行运动协调能力和逻辑思维能力的测试，其测试结果如下表：
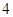人．由于部分数据丢失，只知道从这
．
，
的值；
位，求其中至少有一位运动协调能力或逻辑思维能力优秀的学生的概率；
，求随机变量
．
.