题目内容
甲、乙两人各掷一次骰子(均匀的正方体,六个面上分别为1,2,3,4,5,6点),所得点数分别为x,y
(1)求x<y的概率;
(2)求5<x+y<10的概率。
(1) (2)
(2)
解析试题分析:该问题属古典概型,甲、乙两人各掷一次骰子(均匀的正方体,六个面上分别为1,2,3,4,5,6点),所得点数分别为x,y,有36个基本事件,每个基本事件发生的概率都相等,且互斥;(1)统计出事件“x<y”所包含的基本事件的个数进而求出
(2)统计出事件“5<x+y<10”所包含的基本事件的个数进而求出
试题解析:解:记基本事件为 ,则有
,则有





共36个基本事件
其中满足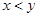 的基本事件有
的基本事件有



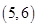
共15个.
满足 的基本事件有
的基本事件有

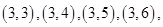


 共20个.
共20个.
(1)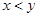 的概率
的概率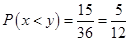
(2) 的概率
的概率
考点:古典概率

练习册系列答案
 轻巧夺冠周测月考直通中考系列答案
轻巧夺冠周测月考直通中考系列答案
相关题目
某商店试销某种商品20天,获得如下数据:
| 日销售量(件) | 0 | 1 | 2 | 3 |
| 频数 | 1 | 5 | 9 | 5 |
试销结束后(假设该商品的日销售量的分布规律不变),设某天开始营业时有该商品3件,当天营业结束后检查存货,若发现存货少于2件,则当天进货补充至3件,否则不进货,将频率视为概率。
(1)求当天商品不进货的概率;
(2)记X为第二天开始营业时该商品的件数,求X的分布列和数学期望。
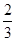 和
和 ,现安排甲组研发新产品
,现安排甲组研发新产品 ,乙组研发新产品
,乙组研发新产品 .设甲,乙两组的研发是相互独立的.
.设甲,乙两组的研发是相互独立的. 万元,若新产品
万元,若新产品 万元,求该企业可获得利润的分布列和数学期望.
万元,求该企业可获得利润的分布列和数学期望. .
. 内任取一个实数
内任取一个实数 ,设事件
,设事件 ={函数
={函数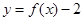 在区间
在区间 上有两个不同的零点},求事件
上有两个不同的零点},求事件 )得到的点数分别为
)得到的点数分别为 ,记事件
,记事件 {
{ 在
在 恒成立},求事件
恒成立},求事件 发生的概率.
发生的概率. ,每道程序中得优、良、中的概率分别为p1、
,每道程序中得优、良、中的概率分别为p1、 、p2.
、p2.