题目内容
5.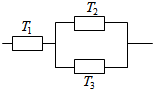 三个元件T1,T2,T3正常工作的概率分别为$\frac{1}{2}\;,\frac{3}{4}\;,\frac{3}{4}$,将它们中某两个元件并联后再和第三个元件串联接入电路.
三个元件T1,T2,T3正常工作的概率分别为$\frac{1}{2}\;,\frac{3}{4}\;,\frac{3}{4}$,将它们中某两个元件并联后再和第三个元件串联接入电路.(1)在如图的一段电路中,电路不发生故障的概率是多少?
(2)三个元件按要求连成怎样的一段电路时,才能使电路中不发生故障的概率最大?请画出此时的电路图,并说明理由.
分析 (1)记“三个元件T1,T2,T3正常工作”分别为事件A1,A2,A3,电路不发生故障的概率为P1=P[(A2∪A3)•A1]=P(A2∪A3)•P(A1),计算求的结果.
(2)如右图,图1中电路不发生故障的事件为(A1∪A2)•A3,求得电路不发生故障的概率P2=P[(A1∪A2)•A3]=P(A1∪A2)•P(A3)值,可得P2>P1 .在图2中,同理不发生故障概率为P3=P2>P1,命题得证.
解答  解:记“三个元件T1,T2,T3正常工作”分别为事件A1,A2,A3,则$P({A_1})=\frac{1}{2}\;\;,P({A_2})=\frac{3}{4}\;\;,P({A_3})=\frac{3}{4}$.
解:记“三个元件T1,T2,T3正常工作”分别为事件A1,A2,A3,则$P({A_1})=\frac{1}{2}\;\;,P({A_2})=\frac{3}{4}\;\;,P({A_3})=\frac{3}{4}$.
(1)电路不发生故障的事件为(A2∪A3)•A1,
∴电路不发生故障的概率为P1=P[(A2∪A3)•A1]=P(A2∪A3)•P(A1)=$[1-P(\overline{A_2})•P(\overline{A_3})]•P({A_1})$=$[1-\frac{1}{4}×\frac{1}{4}]×\frac{1}{2}=\frac{15}{32}$.
(2)如右图,此时电路不发生故障的概率最大.证明如下:
图1中电路不发生故障的事件为(A1∪A2)•A3,
∴电路不发生故障的概率为P2=P[(A1∪A2)•A3]=P(A1∪A2)•P(A3)=$[1-P(\overline{A_1})•P(\overline{A_2})]•P({A_3})$=$[1-\frac{1}{2}×\frac{1}{4}]×\frac{3}{4}=\frac{21}{32}$,
∴P2>P1 .
图2不发生故障事件为(A1∪A3)•A2,同理不发生故障概率为P3=P2>P1,命题得证.
点评 本题主要考查相互独立事件的概率乘法公式,所求的事件的概率与它的对立事件的概率之间的关系,属于基础题.

| A. | $\frac{5}{18}$ | B. | $\frac{5}{9}$ | C. | $\frac{1}{2}$ | D. | $\frac{1}{4}$ |
| A. | 1 | B. | e-1 | C. | e | D. | e+1 |
| A. | ${(\frac{1}{3})^2}×{(\frac{2}{3})^3}$ | B. | ${(\frac{2}{3})^2}×{(\frac{1}{3})^3}$ | C. | $C_5^2{(\frac{2}{3})^2}×{(\frac{1}{3})^3}$ | D. | $C_5^2{(\frac{1}{3})^2}×{(\frac{2}{3})^3}$ |
| 甲 | 80 | 110 | 120 | 140 | 150 |
| 乙 | 100 | 120 | x | 100 | 160 |
(1)从被检测的5辆甲品牌轻型汽车中任取2辆,求至少有一辆二氧化碳排放量超标的概率多少?
(2)求表中x的值,并比较甲、乙两品牌轻型汽车二氧化碳排放量的稳定性.
| A. | -2015 | B. | 2015 | C. | $\frac{2014}{e}$ | D. | -$\frac{2014}{e}$ |