题目内容
17．已知f（x）=$\frac{x}{{e}^{x}}$，定义f1（x）=f′（x），f2（x）=[f1（x）]′，…，fn+1（x）=[fn（x）]′，n∈N．经计算f1（x）=$\frac{1-x}{{e}^{x}}$，f2（x）=$\frac{x-2}{{e}^{x}}$，f3（x）=$\frac{3-x}{{e}^{x}}$，…，照此规律，则f2015（0）=（ ）| A． | -2015 | B． | 2015 | C． | $\frac{2014}{e}$ | D． | -$\frac{2014}{e}$ |
分析 根据归纳推理进行求解即可．
解答 解：∵f1（x）=$\frac{1-x}{{e}^{x}}$，
f2（x）=$\frac{x-2}{{e}^{x}}$，
f3（x）=$\frac{3-x}{{e}^{x}}$，
…，
照此规律，
f2015（x）=$\frac{2015-x}{{e}^{x}}$，
则f2015（x）=$\frac{2015-0}{{e}^{0}}$=2015，
故选：B
点评 本题主要考查函数值的计算，利用归纳推理是解决本题的关键．
练习册系列答案
教材全解字词句篇系列答案
相关题目
8．已知平面中三点A（-1，-1），B（1，2），C（8，-2），判断三角形ABC的形状（ ）
| A． | 锐角三角形 | B． | 直角三角形 | C． | 钝角三角形 | D． | 无法判断 |
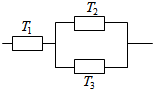三个元件T1，T2，T3正常工作的概率分别为$\frac{1}{2}\;，\frac{3}{4}\;，\frac{3}{4}$，将它们中某两个元件并联后再和第三个元件串联接入电路．