题目内容
16．10个篮球队中有2个强队，先任意将这10个队平均分成两组进行比赛，则2个强队不分在同一组的概率是 （ ）| A． | $\frac{5}{18}$ | B． | $\frac{5}{9}$ | C． | $\frac{1}{2}$ | D． | $\frac{1}{4}$ |
分析 先求出平均分成2组的总事件，再求出2个强队在同一组的事件数，从而可得．
解答 解：平均分成2组的总事件为$\frac{{C}_{10}^{5}}{{A}_{2}^{2}}$=126种，
求出2个强队在同一组的事件为C83=56种，
故则2个强队不分在同一组的概率是1-$\frac{56}{126}$=$\frac{5}{9}$，
故选：B
点评 本题主要考查古典概型的概率问题，关键是分别求出各事件数，属于基础题．
练习册系列答案
相关题目
8．已知平面中三点A（-1，-1），B（1，2），C（8，-2），判断三角形ABC的形状（ ）
| A． | 锐角三角形 | B． | 直角三角形 | C． | 钝角三角形 | D． | 无法判断 |
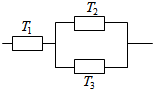三个元件T1，T2，T3正常工作的概率分别为$\frac{1}{2}\;，\frac{3}{4}\;，\frac{3}{4}$，将它们中某两个元件并联后再和第三个元件串联接入电路．