${∫} {0}^{1}$(ex+2x)dx=( )A．1B．e-1C．eD．e+1 题目和参考答案——青夏教育精英家教网——

题目内容

13．${∫}_{0}^{1}$（e^x+2x）dx=（　　）

A．

1

B．

e-1

C．

e

D．

e+1

分析首先找出被积函数的原函数，然后计算．

解答解：${∫}_{0}^{1}$（e^x+2x）dx=（e^x+x²）${|}_{0}^{1}$=e；
故答案为：C

点评本题考查了定积分的计算；关键是正确找出被积函数的原函数．

练习册系列答案

1加1阅读好卷系列答案

专项复习训练系列答案

初中语文教与学阅读系列答案

阅读快车系列答案

完形填空与阅读理解周秘计划系列答案

英语阅读理解150篇系列答案

奔腾英语系列答案

标准阅读系列答案

53English系列答案

考纲强化阅读系列答案

相关题目

3．化简：sin（$\frac{4n-1}{4}$π-α）+cos（$\frac{4n+1}{4}$π-α）（n∈Z）值（　　）

4．设命题p：函数y=lg（ax²+2x+a）的值域为R；命题q：存在x∈[1，3]使x²-2ax+4≤0成立，．如果命题“p∨q”为真命题，“p∧q”为假命题，求a的取值范围．

1．（1）曲线C的极坐标方程为$ρcos（θ-\frac{π}{3}）=\frac{1}{2}$，以极点O为原点，极轴Ox为x的非负半轴，保持单位长度不变建立直角坐标系xoy．求曲线C的直角坐标方程；
（2）已知直线l经过点P（1，1），倾斜角α=$\frac{π}{6}$，
①写出直线l的参数方程．
②设l与圆x²+y²=4相交与两点A，B，求点P到A，B两点的距离之积．

8．已知平面中三点A（-1，-1），B（1，2），C（8，-2），判断三角形ABC的形状（　　）

锐角三角形

直角三角形

钝角三角形

如图所示，将一矩形花坛ABCD扩建成一个更大的矩形花坛AMPN，要求M在AB的延长线上，N在AD的延长线上，且对角线MN过C点．已知AB=3米，AD=2米．设AN=x（单位：米），若x∈[3，4]（单位：米），则当AM，AN的长度分别是多少时，花坛AMPN的面积最大？并求出最大面积．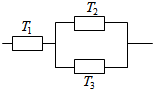

三个元件T₁，T₂，T₃正常工作的概率分别为$\frac{1}{2}\;，\frac{3}{4}\;，\frac{3}{4}$，将它们中某两个元件并联后再和第三个元件串联接入电路．
（1）在如图的一段电路中，电路不发生故障的概率是多少？
（2）三个元件按要求连成怎样的一段电路时，才能使电路中不发生故障的概率最大？请画出此时的电路图，并说明理由．

2．函数y=sin（cosx）的单调递减区间为[2kπ，2kπ+π]，k∈Z．

3．若数列{a_n}满足a₁a₂a₃…a_n=n²+3n+2，在数列{a_n}的通项公式为a_n=$\left\{\begin{array}{l}{6，n=1}\\{\frac{n+2}{n}，n≥2}\end{array}\right.$．