��Ŀ����
4������ڳ��±����ҹ��Ĵ�ͳϰ�ף����������±���У��������װ��2�������±���2����ɳ�±���2�������±����������װ��3�������±���3����ɳ�±�����12���±������ȫ��ͬ���������ѡȡ4�����������¼�AΪ��ѡȡ��4���±���ǡ��2�������±�������2�������±�ѡ��ͬһ����С������¼�A�����ĸ��ʣ�
������XΪѡȡ��4���±��ж�ɳ�±��ĸ��������������X�ķֲ��к���ѧ������
���� �����������֪ʶȷ�������¼��ĸ�����Ȼ�����ùŵ�����ʼ��㹫ʽ�ô𰸣�
�����������X�����п���ȡֵΪ0��1��2��3��4���ɹŵ�����ʼ��㹫ʽ��ø��ʣ��г��ֲ��У�����������ʽ��������
��� �⣺��������֪��$P��A��=\frac{C_2^2C_7^2+C_3^2C_7^2}{{C_{12}^4}}=\frac{28}{165}$��
�����¼�A�����ĸ���Ϊ$\frac{28}{165}$��
����X�����п���ȡֵΪ0��1��2��3��4��
$P��X=0��=\frac{C_5^0C_7^4}{{C_{12}^4}}=\frac{7}{99}$��$P��X=1��=\frac{C_5^1C_7^3}{{C_{12}^4}}=\frac{35}{99}$��
$P��X=2��=\frac{C_5^2C_7^2}{{C_{12}^4}}=\frac{14}{33}$��$P��X=3��=\frac{C_5^3C_7^1}{{C_{12}^4}}=\frac{14}{99}$��$P��X=4��=\frac{C_5^4}{{C_{12}^4}}=\frac{1}{99}$
�����������X�ķֲ���Ϊ
| X | 0 | 1 | 2 | 3 | 4 |
| P | $\frac{7}{99}$ | $\frac{35}{99}$ | $\frac{14}{33}$ | $\frac{14}{99}$ | $\frac{1}{99}$ |
���� ����������ϡ��ŵ���͡���������ķֲ��м���ѧ�������������ø���֪ʶ�����ʵ����������������е��⣮

��ϰ��ϵ�д�
 �Ƹ�С״Ԫͬ������������ϵ�д�
�Ƹ�С״Ԫͬ������������ϵ�д�
�����Ŀ
12����sin��•cos�ȣ�0��|cos��|=cos�ȣ����P��tan�ȣ�cos�ȣ��ڣ�������
| A�� | ��һ���� | B�� | �ڶ����� | C�� | �������� | D�� | �������� |
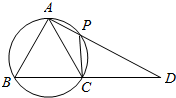 ��ͼ��ʾ�����ı���ABCP�У��߶�AP��BC���ӳ��߽��ڵ�D����֪AB=AC��A��B��C��P�ĵ㹲Բ��
��ͼ��ʾ�����ı���ABCP�У��߶�AP��BC���ӳ��߽��ڵ�D����֪AB=AC��A��B��C��P�ĵ㹲Բ��