题目内容

1．解不等式：$\sqrt{2}$+2cosx≥0．

分析 由题意结合余弦函数的图象可得．

解答 解：原不等式可化为cosx≥-$\frac{\sqrt{2}}{2}$，
∴2kπ-$\frac{3π}{4}$≤x≤2kπ+$\frac{3π}{4}$，
∴原不等式的解集为：{x|2kπ-$\frac{3π}{4}$≤x≤2kπ+$\frac{3π}{4}$，k∈Z}

点评 本题考查三角函数不等式的解集，属基础题．

练习册系列答案
相关题目
11．若tanα=2，则1+sinαcosα=$\frac{7}{5}$．
12．若sinθ•cosθ＜0，|cosθ|=cosθ，则点P（tanθ，cosθ）在（　　）
A．第一象限B．第二象限C．第三象限D．第四象限
9．已知函数y=Asin（ωx+φ）（A＞0，ω＞0，0＜φ＜$\frac{π}{2}$）且y=f（x）的最大值为2，其图象相邻两对称轴的距离为3，并过点（1，2），求y=f（x）的表达式．
16．已知△ABC的三个顶点的坐标分别为A（3，4），B（5，2），C（-1，-4），则这个三角形是（　　）
A．锐角三角形B．直角三角形C．钝角三角形D．等腰直角三角形
6．若x，y满足约束条件$\left\{\begin{array}{l}{x≤2}\\{y≤2}\\{x+y≥2}\end{array}\right.$，则z=x-2y的最小值为-4．
13．函数f（x）=$\sqrt{2-|x-1|}$的定义域是[-1，3]．
12．在Rt△ABC中，AB⊥AC，则有AB2+AC2=BC2成立．拓展到空间，在直四面体P-ABC中，PA⊥PB、PB⊥PC、PC⊥PA．类比平面几何的勾股定理，在直四面体P-ABC中可得到相应的结论是$S_{△ABC}^2=S_{△PAB}^2+S_{△PBC}^2+S_{△PCA}^2$．
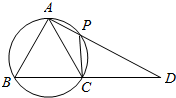13．如图所示，在四边形ABCP中，线段AP与BC的延长线交于点D，已知AB=AC且A，B，C，P四点共圆．
（1）求证：AC•DP=BD•PC
（2）若△ABC是面积为4$\sqrt{3}$的等边三角形，求AP•AD的值．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网