题目内容
2.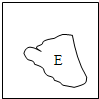 如图边长为2的正方形内部有一块不规则的区域E,若向该图中随机撒100颗豆子,经清点落在E内的有30颗,试估计E的面积为:1.2.
如图边长为2的正方形内部有一块不规则的区域E,若向该图中随机撒100颗豆子,经清点落在E内的有30颗,试估计E的面积为:1.2.
分析 先求出正方形的面积为22,设阴影部分的面积为x,由概率的几何概型知$\frac{30}{100}=\frac{x}{{2}^{2}}$,由此能求出该阴影部分的面积.
解答 解:设阴影部分的面积为x,
由概率的几何概型知,则$\frac{30}{100}=\frac{x}{{2}^{2}}$,
解得x=1.2.
故答案为:1.2.
点评 本题考查概率的性质和应用;每个事件发生的概率只与构成该事件区域的长度(面积或体积)成比例,则称这样的概率模型为几何概型.

练习册系列答案
相关题目
10.若[x]表示不超过x的最大整数,例如[2.9]=2,[-4.1]=-5,已知f(x)=x-[x](x∈R),g(x)=log2015x,则函数h(x)=f(x)-g(x)的零点个数是( )
| A. | 2016 | B. | 2015 | C. | 2014 | D. | 2013 |
7.下列命题中,错误的是( )
| A. | 一条直线与两个平行平面中的一个相交,则必与另一个相交 | |
| B. | 平行于同一直线的两个平面平行 | |
| C. | 平行于同一平面的两个平面平行 | |
| D. | 一个平面与两个平行平面相交,交线平行 |
12.集合P={x|y=$\sqrt{x+1}$},Q={y|y=$\sqrt{x+1}$},则P,Q的关系是( )
| A. | P=Q | B. | P?Q | C. | Q?P | D. | P∩Q=∅ |
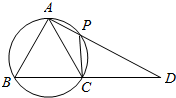 如图所示,在四边形ABCP中,线段AP与BC的延长线交于点D,已知AB=AC且A,B,C,P四点共圆.
如图所示,在四边形ABCP中,线段AP与BC的延长线交于点D,已知AB=AC且A,B,C,P四点共圆.