题目内容
2.若不等式${x^2}-2{log_a}x≤0在x∈(0,\frac{{\sqrt{2}}}{2}]$恒成立,则实数a的最小值为$\frac{1}{4}$.分析 不等式整理为$\frac{1}{2}$x2≤logax在x∈(0,$\frac{\sqrt{2}}{2}$]时恒成立,只需$\frac{1}{2}$x2的最大值小于logax的最小值,利用分类讨论对a讨论即可.
解答 解:不等式${x^2}-2{log_a}x≤0在x∈(0,\frac{{\sqrt{2}}}{2}]$恒成立,
即为$\frac{1}{2}$x2≤logax在x∈(0,$\frac{\sqrt{2}}{2}$]时恒成立,
∴$\frac{1}{2}$x2的最大值小于logax的最小值.
∴$\frac{1}{2}$x2≤$\frac{1}{4}$≤logax,
当a>1时,logax为递增,但最小值为负数不成立.
当0<a<1时,logax为递减,
最小值在x=$\frac{\sqrt{2}}{2}$上取到,
∴loga $\frac{\sqrt{2}}{2}$≥$\frac{1}{4}$=loga$\frac{1}{4}$,
∴a≥$\frac{1}{4}$,
故a的最小值为$\frac{1}{4}$.
故答案为:$\frac{1}{4}$.
点评 本题考查不等式恒成立问题的解法,注意运用对数函数的单调性和恒成立思想,考查运算能力,属于中档题.

练习册系列答案
相关题目
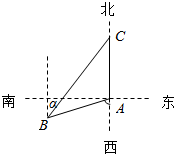 如图,渔船甲位于岛屿A的南偏西60°方向的B处,且与岛屿A相距12海里,渔船乙以10海里/小时的速度从岛屿A出发沿正北方向航行,若渔船甲同时从B处出发沿北偏东α的方向在C处追赶上渔船乙,刚好用2小时.则BC=28.
如图,渔船甲位于岛屿A的南偏西60°方向的B处,且与岛屿A相距12海里,渔船乙以10海里/小时的速度从岛屿A出发沿正北方向航行,若渔船甲同时从B处出发沿北偏东α的方向在C处追赶上渔船乙,刚好用2小时.则BC=28.