题目内容
17．在等差数列{an}中，已知a2+a9=7，则3a5+a7=14．分析 由已知求得2a1+9d=7，把3a5+a7转化为含有2a1+d的形式得答案．
解答 解：在等差数列{an}中，由a2+a9=7，得a1+d+a1+8d=7，
即2a1+9d=7，
∴3a5+a7=3（a1+4d）+a1+6d=2（2a1+9d）=2×7=14．
故答案为：14．
点评 本题考查等差数列的通项公式，体现了整体运算思想方法，是基础题．
练习册系列答案
A加金题 系列答案
全优测试卷系列答案
相关题目
8．△ABC中，sinA：sinB：sinC=3：5：7，则△ABC中最大角的度数是（ ）
| A． | 150° | B． | 120° | C． | 90° | D． | 135° |
5．连续抛掷两次骰子，所得的点数之和能被3整除的概率为（ ）
| A． | $\frac{1}{6}$ | B． | $\frac{1}{3}$ | C． | $\frac{11}{36}$ | D． | $\frac{5}{6}$ |
9．已知集合A={x∈N|x＜8}，则下列关系错误的是（ ）
| A． | 0∈A | B． | 1.5∉A | C． | -1∉A | D． | 8∈A |
6．
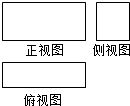某长方体的三视图如图，长度为$\sqrt{10}$的体对角线在正视图中的投影长度为$\sqrt{6}$，在侧视图中的投影长度为$\sqrt{5}$，则该长方体的全面积为（ ）
某长方体的三视图如图，长度为$\sqrt{10}$的体对角线在正视图中的投影长度为$\sqrt{6}$，在侧视图中的投影长度为$\sqrt{5}$，则该长方体的全面积为（ ）| A． | 3$\sqrt{5}$+2 | B． | 6$\sqrt{5}$+4 | C． | 6 | D． | 10 |