题目内容
12.下列命题中正确命题的个数是(1)对于命题p:?x∈R,使得x2+x+1<0,则¬p:?x∈R,均有x2+x+1>0;
(2)命题“已知x,y∈R,若x+y≠3,则x≠2或y≠1”是真命题
(3)回归直线的斜率的估计值为1.23,样本点的中心为(4,5),则回归直线方程为$\hat y$=1.23x+0.08
(4)m=3是直线(m+3)x+my-2=0与直线mx-6y+5=0互相垂直的充要条件;
(5)若a,b∈[0,1],则不等式a2+b2<$\frac{1}{4}$ 成立的概率是$\frac{π}{4}$;( )
| A. | 4 | B. | 3 | C. | 2 | D. | 1 |
分析 写出命题的否定判断(1);写出原命题的逆否命题并判断真假判断(2);直接求出回归直线方程判断(3);利用充分必要条件的判定方法判断(4);求出几何概型的概率判断(5).
解答 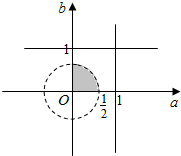 解:(1)对于命题p:?x∈R,使得x2+x+1<0,则¬p:?x∈R,均有x2+x+1≥0,故(1)错误;
解:(1)对于命题p:?x∈R,使得x2+x+1<0,则¬p:?x∈R,均有x2+x+1≥0,故(1)错误;
(2)命题“已知x,y∈R,若x+y≠3,则x≠2或y≠1”的逆否命题是:“已知x,y∈R,若x=2且y=1,则x+y=3”是真命题,
∴原命题是真命题,故(2)正确;
(3)∵回归直线方程一定过样本中心点,且回归直线的斜率的估计值为1.23,∴5=$\widehat{a}$+1.23×4,解得$\widehat{a}$=0.08,
∴这组数据对应的线性回归方程是$\hat y$=1.23x+0.08,故(3)正确;
(4)由m(m+3)-6m=0,解得m=0或m=3,∴m=3是直线(m+3)x+my-2=0与直线mx-6y+5=0互相垂直的充分不必要条件,故(4)错误;
(5)如图,a,b∈[0,1],则不等式a2+b2<$\frac{1}{4}$ 成立的概率是$\frac{\frac{1}{4}×\frac{π}{4}}{1}=\frac{π}{16}$,故(5)错误.
∴正确命题的个数是2个.
故选:C.
点评 本题考查命题的真假判断与应用,考查命题的否定和逆否命题,考查了线性回归方程的求法,训练了几何概型概率的求法,是中档题.

练习册系列答案
相关题目
3.函数f(x)=[x]的函数值表示不超过x的最大整数,例如[-3.5]=-4,[2.1]=2,则函数f(x)=[x],x∈[-2,3]与直线y=x(x∈R)的交点个数( )
| A. | 5个 | B. | 6个 | C. | 7个 | D. | 8个 |
17.不等式$\frac{3-4x}{1-2x}$≤1的解集为( )
| A. | [1,+∞) | B. | ($\frac{1}{2}$,1) | C. | [$\frac{1}{2}$,1] | D. | ($\frac{1}{2}$,1] |
2.下面几个空间图形中,虚线、实线使用不正确的有( )
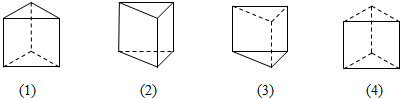

| A. | (2)(3) | B. | (1)(3) | C. | (3)(4) | D. | (4) |