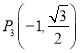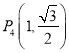Question

【题目】如图在四面体ABCD中，若截面PQMN是正方形，则在下列命题中正确的有 ．（填上所有正确命题的序号）
①AC⊥BD
②AC=BD
③AC∥截面PQMN
④异面直线PM与BD所成的角为45°．

Answer 1

【答案】①③④
【解析】解：在四面体ABCD中，∵截面PQMN是正方形，∴PQ∥MN，PQ平面ACD，MN平面ACD，∴PQ∥平面ACD．
∵平面ACB∩平面ACD=AC，∴PQ∥AC，可得AC∥平面PQMN．
同理可得BD∥平面PQMN，BD∥PN．
∵PN⊥PQ，∴AC⊥BD．
由BD∥PN，
∴∠MPN是异面直线PM与BD所成的角，且为45°．
由上面可知：BD∥PN，PQ∥AC．
∴
而AN≠DN，PN=MN，
∴BD≠AC．
综上可知：①③④都正确．
所以答案是：①③④．
【考点精析】根据题目的已知条件，利用命题的真假判断与应用和异面直线及其所成的角的相关知识可以得到问题的答案，需要掌握两个命题互为逆否命题，它们有相同的真假性；两个命题为互逆命题或互否命题，它们的真假性没有关系；异面直线所成角的求法：1、平移法：在异面直线中的一条直线中选择一特殊点，作另一条的平行线；2、补形法：把空间图形补成熟悉的或完整的几何体，如正方体、平行六面体、长方体等，其目的在于容易发现两条异面直线间的关系．