题目内容
【题目】已知椭圆![]() (
(![]() ),四点
),四点![]() ,
, ![]() ,
, 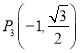 ,
, 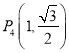 中恰有三点在椭圆上.
中恰有三点在椭圆上.
(1)求![]() 的方程;
的方程;
(2)设直线![]() 不经过
不经过![]() 点且与
点且与![]() 相交于
相交于![]() 两点,若直线
两点,若直线![]() 与直线
与直线![]() 的斜率之和为
的斜率之和为![]() ,证明:
,证明: ![]() 过定点.
过定点.
【答案】(1)![]() ;(2)见解析.
;(2)见解析.
【解析】试题分析:(1)根据椭圆的对称性,得到![]() ,
, 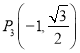 ,
, 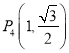 , 三点在椭圆C上.把点坐标代入椭圆C,求出a2=4,b2=1,由此能求出椭圆C的方程.
, 三点在椭圆C上.把点坐标代入椭圆C,求出a2=4,b2=1,由此能求出椭圆C的方程.
(2)设直线l: ![]() ,,不设直线P2A与直线P2B的斜率分别为k1,k2, 联立直线P2A与椭圆方程得
,,不设直线P2A与直线P2B的斜率分别为k1,k2, 联立直线P2A与椭圆方程得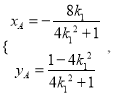 代入直线l方程:
代入直线l方程: ![]() 中得
中得![]() ,同理
,同理![]() ,所以易知k1,k2 ,是方程
,所以易知k1,k2 ,是方程![]() 两根,由韦达定理
两根,由韦达定理![]() ,即可得解.
,即可得解.
试题解析:
(1)由于p3,p4两点关于y轴对称,故由题设知C经过p3,p4两点,又由![]() 知,C不经过点
知,C不经过点 ![]() ,所以点
,所以点![]() 在C上
在C上
因此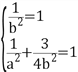 ,解得
,解得![]()
故C的方程为![]()
(2)由题设易知,直线l与x轴不平行,故可设方程为:![]() ,
,
设直线P2A与直线P2B的斜率分别为k1,k2 ,
联立直线P2A与椭圆方程 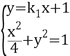
![]()
即![]() 代入
代入![]() 直线方程得
直线方程得![]() .
.
即 代入直线l方程:
代入直线l方程: ![]() 中,
中,
化简得:![]()
同理: ![]()
易知k1,k2 ,是方程![]() 两根
两根
故k1+k2 =![]()
![]() m=t+2
m=t+2
即直线l为:![]()
![]()
即l过定点(2,-1).

练习册系列答案
相关题目
【题目】某手机卖场对市民进行国产手机认可度的调查,随机抽取![]() 名市民,按年龄(单位:岁)进行统计和频数分布表和频率分布直线图如下:
名市民,按年龄(单位:岁)进行统计和频数分布表和频率分布直线图如下:
分组(岁) | 频数 |
|
|
|
|
|
|
|
|
|
|
合计 |
|
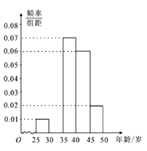
(1)求频率分布表中![]() 、
、![]() 的值,并补全频率分布直方图;
的值,并补全频率分布直方图;
(2)在抽取的这![]() 名市民中,按年龄进行分层抽样,抽取
名市民中,按年龄进行分层抽样,抽取![]() 人参加国产手机用户体验问卷调查,现从这
人参加国产手机用户体验问卷调查,现从这![]() 人中随机选取
人中随机选取![]() 人各赠送精美礼品一份,设这
人各赠送精美礼品一份,设这![]() 名市民中年龄在
名市民中年龄在![]() 内的人数
内的人数![]() ,求
,求![]() 的分布列及数学期望.
的分布列及数学期望.