题目内容
【题目】求满足下列条件的直线的方程：
（1）经过两条直线2x﹣3y+10=0和3x+4y﹣2=0的交点，且垂直于直线3x﹣2y+4=0；
（2）经过两条直线2x+y﹣8=0和x﹣2y+1=0的交点，且平行于直线4x﹣3y﹣7=0．
【答案】解：（1）联立
，解得
，
∴两条直线2x﹣3y+10=0和3x+4y﹣2=0的交点为（﹣2，2），
又直线3x﹣2y+4=0的斜率为
，
∴经过两条直线2x﹣3y+10=0和3x+4y﹣2=0的交点，且垂直于直线3x﹣2y+4=0的直线方程为：
y﹣2=-（x+2），即2x+3y﹣2=0；
（2）联立
，解得
．
∴两条直线2x+y﹣8=0和x﹣2y+1=0的交点坐标为（3，2），
又直线4x﹣3y﹣7=0的斜率为
，
∴经过两条直线2x+y﹣8=0和x﹣2y+1=0的交点，且平行于直线4x﹣3y﹣7=0的直线方程为：
y﹣2=（x﹣3），即4x﹣3y﹣6=0．
【解析】（1）联立两直线方程求得两直线交点，由直线与直线3x﹣2y+4=0垂直求得斜率，代入直线方程的点斜式得答案；
（2）联立两直线方程求得两直线交点，由直线与直线4x﹣3y﹣7=0平行求得斜率，代入直线方程的点斜式得答案．
练习册系列答案
相关题目
【题目】某手机卖场对市民进行国产手机认可度的调查，随机抽取
名市民，按年龄（单位：岁）进行统计和频数分布表和频率分布直线图如下：
分组（岁） | 频数 |
|
|
|
|
|
|
|
|
|
|
合计 |
|
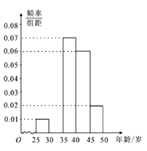
（1）求频率分布表中
、
的值，并补全频率分布直方图；
（2）在抽取的这
名市民中，按年龄进行分层抽样，抽取
人参加国产手机用户体验问卷调查，现从这
人中随机选取
人各赠送精美礼品一份，设这
名市民中年龄在
内的人数
，求
的分布列及数学期望.
