题目内容
【题目】数列![]() 的前
的前![]() 项和为
项和为![]() , 已知
, 已知![]() ,且
,且![]() ,
, ![]() ,
, ![]() 三个数依次成等差数列.
三个数依次成等差数列.
(Ⅰ)求![]() 的值;
的值;
(Ⅱ)求数列![]() 的通项公式;
的通项公式;
(Ⅲ)若数列![]() 满足
满足![]() ,设
,设![]() 是其前
是其前![]() 项和,求证:
项和,求证: ![]() .
.
【答案】(I)![]() ;(II)
;(II)![]() ;(Ⅲ)见解析.
;(Ⅲ)见解析.
【解析】试题分析:(1)先由和项与通项关系得项之间递推关系式,再依次求![]() ,根据等差中项性质列方程,解得
,根据等差中项性质列方程,解得![]() 的值;(2)将项之间递推关系式进行整理变形为
的值;(2)将项之间递推关系式进行整理变形为![]() ,根据等比数列定义以及通项公式求得
,根据等比数列定义以及通项公式求得![]() ,即得数列
,即得数列![]() 的通项公式;(3)先化简得
的通项公式;(3)先化简得![]() ,再从第三项起放缩并利用裂项相消法求和得
,再从第三项起放缩并利用裂项相消法求和得![]() .
.
试题解析:(Ⅰ)由已知![]() ,得
,得
当![]() 时,
时, ![]() ,
, ![]() ①
①
当![]() 时,
时, ![]() ,
, ![]() ②
②
又∵![]() 成等差数列,∴
成等差数列,∴![]() ③
③
将①、②代入③解得: ![]()
(Ⅱ)由![]() 得:
得: ![]()
∴![]() 即
即![]()
∴![]() ,
,
∴![]() 是以
是以![]() 为首项,2为公比的等比数列
为首项,2为公比的等比数列
∴![]() ,
,
∴![]() .
.
(Ⅲ)由![]() 得:
得: ![]()
①当![]() 时,
时, ![]() ,
,
②当![]() 时,
时, ![]() ,
,
③当![]() ,
, ![]() 时,
时, ![]() ,
,
∴![]()
![]()
![]()
![]() .
.
综上所述,当![]() 时,
时, ![]() .
.

【题目】某校高三年级共有学生195人,其中女生105人,男生90人.现采用按性别分层抽样的方法,从中抽取13人进行问卷调查.设其中某项问题的选择分别为“同意”、“不同意”两种,且每人都做了一种选择.下面表格中提供了被调查人答卷情况的部分信息.
同意 | 不同意 | 合计 | |
女学生 | 4 | ||
男学生 | 2 |
(Ⅰ)完成上述统计表;
(Ⅱ)根据上表的数据估计高三年级学生该项问题选择“同意”的人数;
(Ⅲ) 从被抽取的女生中随机选取2人进行访谈,求选取的2名女生中至少有一人选择“同意”的概率.
【题目】某手机卖场对市民进行国产手机认可度的调查,随机抽取![]() 名市民,按年龄(单位:岁)进行统计和频数分布表和频率分布直线图如下:
名市民,按年龄(单位:岁)进行统计和频数分布表和频率分布直线图如下:
分组(岁) | 频数 |
|
|
|
|
|
|
|
|
|
|
合计 |
|
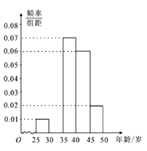
(1)求频率分布表中![]() 、
、![]() 的值,并补全频率分布直方图;
的值,并补全频率分布直方图;
(2)在抽取的这![]() 名市民中,按年龄进行分层抽样,抽取
名市民中,按年龄进行分层抽样,抽取![]() 人参加国产手机用户体验问卷调查,现从这
人参加国产手机用户体验问卷调查,现从这![]() 人中随机选取
人中随机选取![]() 人各赠送精美礼品一份,设这
人各赠送精美礼品一份,设这![]() 名市民中年龄在
名市民中年龄在![]() 内的人数
内的人数![]() ,求
,求![]() 的分布列及数学期望.
的分布列及数学期望.