题目内容
在空间四边形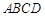 中,
中, 、
、 、
、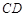 、
、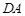 上分别取
上分别取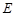 、
、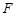 、
、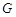 、
、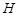 四点,
四点,
如果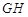 、
、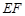 交于一点
交于一点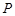 ,则( )
,则( )
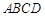 中,
中,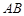 、
、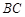 、
、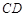 、
、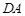 上分别取
上分别取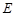 、
、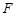 、
、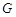 、
、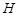 四点,
四点,如果
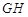 、
、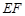 交于一点
交于一点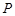 ,则( )
,则( )A.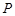 一定在直线 一定在直线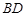 上 上 | B.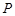 一定在直线 一定在直线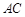 上 上 |
C.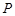 在直线 在直线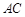 或 或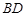 上 上 | D.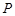 既不在直线 既不在直线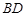 上,也不在 上,也不在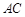 上 上 |
B
先根据EF、GH相交于点P得到点P属于直线EF,且属于直线GH,再根据EF属于面ABC,GH属于面ADC即可得到点P必在面ABC与面ADC的交线上,进而得到结论.
解:EF、GH相交于点P,
则点P属于直线EF,且属于直线GH.
又由题意,EF属于面ABC,GH属于面ADC
则点P即属于面ABC,又属于面ADC
则点P必在面ABC与面ADC的交线上,即
点P必在AC上.
故选B.
解:EF、GH相交于点P,
则点P属于直线EF,且属于直线GH.
又由题意,EF属于面ABC,GH属于面ADC
则点P即属于面ABC,又属于面ADC
则点P必在面ABC与面ADC的交线上,即
点P必在AC上.
故选B.

练习册系列答案
相关题目
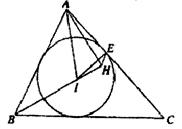
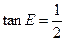 ,⊙O的半径为3,求OA的长。
,⊙O的半径为3,求OA的长。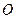 的直径
的直径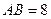 ,
,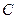 为圆周上一点,
为圆周上一点,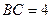 ,过
,过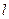 ,过
,过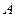 作直线
作直线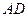 ,
,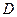 为垂足,
为垂足,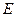 ,则线段
,则线段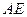 的长为 .
的长为 .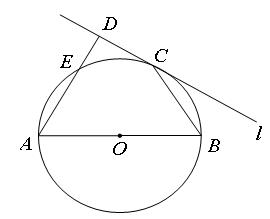
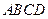 中,
中,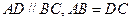 ,过点
,过点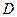 作
作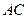 的平行线
的平行线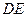 ,交
,交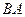 的延长线于点
的延长线于点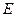 .求证:⑴
.求证:⑴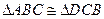 ⑵
⑵ 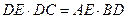
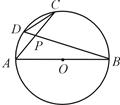
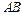 为⊙
为⊙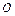 的直径,弦
的直径,弦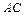 、
、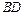 交于点
交于点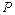 ,若
,若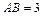 ,
,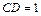 ,则
,则 .
.
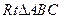 的两条直角边
的两条直角边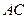 ,
,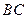 的长分别为
的长分别为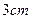 ,
,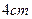 ,以
,以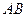 交于点
交于点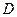 ,则
,则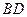 =
= 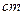 .
.