题目内容
选修41:几何证明选讲
如图,设AB为⊙O的任意一条不与直线l垂直的直径,P是⊙O与l的公共点,AC⊥l,BD⊥l,垂足分别为C,D,且PC=PD.
求证:(1) l是⊙O的切线;(2) PB平分∠ABD.
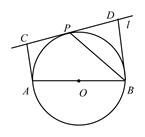
如图,设AB为⊙O的任意一条不与直线l垂直的直径,P是⊙O与l的公共点,AC⊥l,BD⊥l,垂足分别为C,D,且PC=PD.
求证:(1) l是⊙O的切线;(2) PB平分∠ABD.

(1) 连接OP,∵AC⊥l,BD⊥l,∴AC∥BD.
又OA=OB,PC=PD,∴OP∥BP,从而OP⊥l.
∵P在⊙O上,∴l是⊙O的切线.(6分)
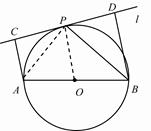
(2) 连接AP,∵l是⊙O的切线,
∴∠BPD=∠BAP.
又∠BPD+∠PBD=90°,∠BAP+∠PBA=90°,
∴∠PBA=∠PBD,即PB平分∠ABD.(10分)
又OA=OB,PC=PD,∴OP∥BP,从而OP⊥l.
∵P在⊙O上,∴l是⊙O的切线.(6分)

(2) 连接AP,∵l是⊙O的切线,
∴∠BPD=∠BAP.
又∠BPD+∠PBD=90°,∠BAP+∠PBA=90°,
∴∠PBA=∠PBD,即PB平分∠ABD.(10分)
略

练习册系列答案
 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案
相关题目
 中,
中,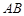 、
、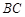 、
、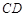 、
、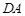 上分别取
上分别取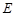 、
、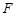 、
、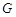 、
、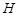 四点,
四点,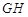 、
、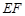 交于一点
交于一点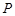 ,则( )
,则( )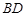 上
上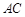 上
上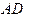 是
是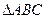 的外角
的外角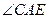 的平分线,交BC的延长线于点D,延长DA交
的平分线,交BC的延长线于点D,延长DA交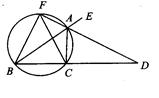
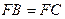 .
.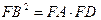 .
.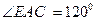 ,BC=6cm,求AD的长.
,BC=6cm,求AD的长.
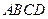 是边长为
是边长为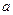 的正方形,以
的正方形,以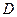 为圆心,
为圆心,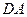 为半径的圆弧与以
为半径的圆弧与以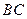 为直径的圆
为直径的圆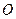 交于点
交于点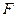 ,连接
,连接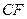 并延长
并延长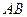 点
点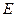
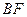 的长
的长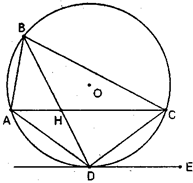
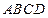 中,
中,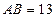 ,三角形
,三角形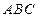 的面积为
的面积为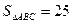 ,
,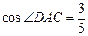 ,
,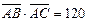 ,
,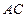 的长; (2)
的长; (2)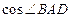

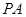 是圆
是圆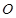 的切线,
的切线,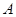 为切点,过
为切点,过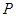 做圆
做圆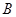 、
、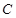 两点,
两点,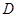 为弦
为弦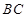 的中点,若圆心
的中点,若圆心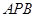 的内部,则∠
的内部,则∠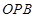 +∠
+∠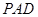 的度数为: ;
的度数为: ;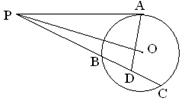
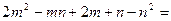 .
.