题目内容

18．对于等比数列{an}前n项和为Sn，S3=2，S6=8，则S9=（　　）
A．32B．18C．26D．34

分析 利用等比数列性质：由{an}为等比数列，得S3，S6-S3，S9-S6成等比数列，由此得到方程，解出即可．

解答 解：因为{an}为等比数列，等比数列{an}前n项和为Sn，S3=2，S6=8，
所以由等比数列的性质知，S3，S6-S3，S9-S6成等比数列，即（S6-S3）2=S3（S9-S6），
所以（8-2）2=2•（S9-8），解得S9=26，
故选：C．

点评 本题考查等比数列的前n项和，考查等比数列的性质，属基础题，灵活应用等比数列的性质是解决本题的关键．

练习册系列答案
相关题目
8．（1）已知tanα=2，求$\frac{sinα+cosα}{sinα-cosα}$的值；
（2）已知$sinα=-\frac{3}{5}$，且α第三象限角，求 $\frac{{sin（2π-α）cos（π+α）cos（\frac{π}{2}+α）cos（\frac{11π}{2}-α）}}{{cos（π-α）sin（3π-α）sin（-π-α）sin（\frac{9π}{2}+α）}}$的值．
9．已知{an}是等比数列，有a3•a11=4a7，{bn}是等差数列，且a7=b7，则b5+b9=（　　）
A．4B．8C．0或8D．16
6．直线y=kx+b与曲线y=x3-3x+1相切于点（2，3），则b的值为（　　）
A．-3B．9C．-7D．-15
13．湛江一中学生会的6名学生会干部按团委的要求分配到三个不同的年级对同学们进行仪容仪表检查，若每个年级安排2名学生会干部，则不同的分配方案有90种．（用数字作答）
3．已知f（x）在实数集R上是单调递增函数，且对任意的实数x1，x2，都有f（x1+x2）=f（x1）f（x2）．
（1）求f（0）的值；
（2）设f（x）的反函数为f-1（x）（x∈A），求证：对于任意的x1，x2∈A，都有f-1（x1x2）=f-1（x1）+f-1（x2）；
（3）求证：对于任意的实数x，都有f（x）＞0．
10．利用计算机在区间（0，1）上产生两个随机数a和b，则方程x=-2a-$\frac{{4{b^2}}}{x}$无实根的概率为$\frac{1}{2}$．
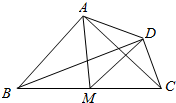7．如图，四边形ABCD满足$\overrightarrow{AB}$•$\overrightarrow{AC}$=$\overrightarrow{DB}$•$\overrightarrow{DC}$=0，|$\overrightarrow{AB}$|=2|$\overrightarrow{DC}$|=2，若M是BC的中点，则$\overrightarrow{AB}$•$\overrightarrow{AM}$-$\overrightarrow{DM}$•$\overrightarrow{DC}$=（　　）
A．1B．-1C．-$\frac{3}{2}$D．$\frac{3}{2}$
8．已知函数f（x）=$\frac{1}{a}$-$\frac{1}{x}$．
（1）用单调性定义证明f（x）在（0，+∞）上是单调递增函数；
（2）若f（x）在[$\frac{1}{4}$，m]上的值域是[$\frac{1}{2}$，2]，求a和m的值．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网