题目内容
8.(1)已知tanα=2,求$\frac{sinα+cosα}{sinα-cosα}$的值;(2)已知$sinα=-\frac{3}{5}$,且α第三象限角,求 $\frac{{sin(2π-α)cos(π+α)cos(\frac{π}{2}+α)cos(\frac{11π}{2}-α)}}{{cos(π-α)sin(3π-α)sin(-π-α)sin(\frac{9π}{2}+α)}}$的值.
分析 (1)直接利用同角三角函数的基本关系式化简求解即可.
(2)利用诱导公式化简然后利用同角三角函数的基本关系式求解即可.
解答 解:(1)tanα=2,
$\frac{sinα+cosα}{sinα-cosα}$=$\frac{tanα+1}{tanα-1}$=$\frac{2+1}{2-1}$=3;
(2)已知$sinα=-\frac{3}{5}$,且α第三象限角,cosα=$-\frac{4}{5}$,tanα=$\frac{3}{4}$,
$\frac{{sin(2π-α)cos(π+α)cos(\frac{π}{2}+α)cos(\frac{11π}{2}-α)}}{{cos(π-α)sin(3π-α)sin(-π-α)sin(\frac{9π}{2}+α)}}$=$-\frac{sinαcosαsinαsinα}{cosαsinαsinαcosα}$=-tanα=-$\frac{3}{4}$.
点评 本题考查诱导公式的应用,三角函数的化简求值,考查计算能力.

练习册系列答案
相关题目
3.某次考试后,甲、乙、丙三位同学被问到是否答对三道填空题时,
甲说:我答对的题数比乙多,但答错第一题;
乙说:我至少答对第二题或第三题中的一题;
丙说:我答错了第三题.
若有一题三人都答对,则该题为第二题.
甲说:我答对的题数比乙多,但答错第一题;
乙说:我至少答对第二题或第三题中的一题;
丙说:我答错了第三题.
若有一题三人都答对,则该题为第二题.
13.在△ABC中,A,B是三角形的内角,且A=90°,若$\overrightarrow{AB}$=(2,-1),$\overrightarrow{AC}$=(sinB,$\sqrt{3}$),则角B等于( )
| A. | 30° | B. | 60° | C. | 60°或120° | D. | 30°或150° |
20.已知|$\overrightarrow{a}$|=1,|$\overrightarrow{b}$|=2,a与b的夹角为120°,且$\overrightarrow{a}$+$\overrightarrow{b}$+$\overrightarrow{c}$=0,则$\overrightarrow{a}$与$\overrightarrow{c}$的夹角为( )
| A. | 30° | B. | 60° | C. | 90° | D. | 150° |
18.对于等比数列{an}前n项和为Sn,S3=2,S6=8,则S9=( )
| A. | 32 | B. | 18 | C. | 26 | D. | 34 |
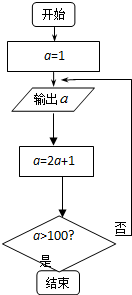 按照如图所示的框图操作,
按照如图所示的框图操作,