题目内容
8.已知函数f(x)=$\frac{1}{a}$-$\frac{1}{x}$.(1)用单调性定义证明f(x)在(0,+∞)上是单调递增函数;
(2)若f(x)在[$\frac{1}{4}$,m]上的值域是[$\frac{1}{2}$,2],求a和m的值.
分析 (1)设任意x2>x1>0,作差得f(x2)-f(x1)>0即可;(2)根据函数的单调性得到不等式组解出即可.
解答 解:(1)证明:设任意x2>x1>0,则x2-x1>0,x1 x2>0,
∵f(x2)-f(x1)=($\frac{1}{a}$-$\frac{1}{{x}_{2}}$)-($\frac{1}{a}$-$\frac{1}{{x}_{1}}$)=$\frac{1}{{x}_{1}}$-$\frac{1}{{x}_{2}}$=$\frac{{x}_{2}{-x}_{1}}{{{x}_{1}x}_{2}}$>0,
∴f(x2)>f(x1),
∴f(x)在(0,+∞)上是单调递增的.
(2)∵f(x)在$[{\frac{1}{4},m}]$上单调递增,
∴$\left\{\begin{array}{l}{f(\frac{1}{4})=\frac{1}{a}-4=\frac{1}{2}}\\{f(m)=\frac{1}{a}-\frac{1}{m}=2}\end{array}\right.$,
易得a=$\frac{2}{9}$,m=$\frac{2}{5}$.
点评 本题考查了函数的单调性的定义问题,考查单调性的应用,本题是一道中档题.

练习册系列答案
相关题目
18.对于等比数列{an}前n项和为Sn,S3=2,S6=8,则S9=( )
| A. | 32 | B. | 18 | C. | 26 | D. | 34 |
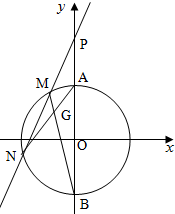 已知A,B为圆O:x2+y2=4与y轴的交点(A在B上),过点P(0,4)的直线l交圆O于M,N两点.
已知A,B为圆O:x2+y2=4与y轴的交点(A在B上),过点P(0,4)的直线l交圆O于M,N两点.