题目内容
10.利用计算机在区间(0,1)上产生两个随机数a和b,则方程x=-2a-$\frac{{4{b^2}}}{x}$无实根的概率为$\frac{1}{2}$.分析 本题考查的知识点是几何概型的意义,关键是要找出(0,1)上产生两个随机数a和b所对就图形的面积,及方程有实根对应的图形的面积,并将其代入几何概型计算公式,进行求解由于是两个变量所以几何概型的概率用不了对应的区域面积表示,利用面积比求概率.
解答 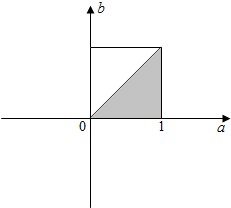 解:设在区间(0,1)上产生两个随机数a和b,记为(a,b),对于区域的面积为边长为1的正方形的面积1,
解:设在区间(0,1)上产生两个随机数a和b,记为(a,b),对于区域的面积为边长为1的正方形的面积1,
而在此条件下满足方程x=-2a-$\frac{{4{b^2}}}{x}$整理得
x2+2ax+b2=0,方程有实根,△≥0
即4a2-4b2≥0
∴b≤a.
在aOb坐标系中画出图形.如图.
∴方程有实根的概率为P=$\frac{{S}_{阴影部分}}{{S}_{正方形}}$=$\frac{1}{2}$
故答案为:$\frac{1}{2}$.
点评 本题考查了几何概型概率的求法;几何概型的概率估算公式中的“几何度量”,可以为线段长度、面积、体积等,而且这个“几何度量”只与“大小”有关,而与形状和位置无关.

练习册系列答案
相关题目
20.已知|$\overrightarrow{a}$|=1,|$\overrightarrow{b}$|=2,a与b的夹角为120°,且$\overrightarrow{a}$+$\overrightarrow{b}$+$\overrightarrow{c}$=0,则$\overrightarrow{a}$与$\overrightarrow{c}$的夹角为( )
| A. | 30° | B. | 60° | C. | 90° | D. | 150° |
18.对于等比数列{an}前n项和为Sn,S3=2,S6=8,则S9=( )
| A. | 32 | B. | 18 | C. | 26 | D. | 34 |