题目内容
在正方体ABCD-A1B1C1D1中，其棱长为2，则异面直线DC与BC1之间的距离为（ ）
| A．1 | B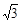． | C．2 | D． |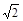
D
解：欲求棱A1B1所在直线与面对角线BC1所在直线间的距离，先找到这两条直线的公垂线段，即与这两条直线都垂直相交的线段，在求出公垂线段的长度即可．
解连接B1C，与BC1交于点O，
∵A1B1⊥平面BC1，B1C?平面BC1，∴A1B1⊥B1C
又∵B1C⊥B1C，B1C∩B1C=O，A1B1∩B1C=B1
∴线段B1O是棱CD所在直线与面对角线BC1的公垂线段．
∵正方体ABCD-A1B1C1D1的棱长为a=2，
∴B1C=2a，B1O=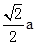
= 
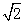
解连接B1C，与BC1交于点O，
∵A1B1⊥平面BC1，B1C?平面BC1，∴A1B1⊥B1C
又∵B1C⊥B1C，B1C∩B1C=O，A1B1∩B1C=B1
∴线段B1O是棱CD所在直线与面对角线BC1的公垂线段．
∵正方体ABCD-A1B1C1D1的棱长为a=2，
∴B1C=2a，B1O=
= 
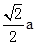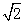
练习册系列答案
相关题目
表示两个不同的平面，l表示既不在a内也不在
内的直线，存在以下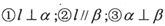
.若以其中两个为条件，另一个为结论，构成命题，
，
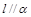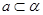，则
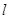与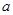
的位置关系一定是（ ）
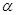没有公共点
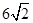
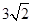
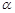∩平面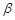
=AB，PQ⊥
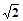，求AB1与C1B所成角的大小。