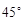题目内容
 表示两个不同的平面,l表示既不在a内也不在
表示两个不同的平面,l表示既不在a内也不在 内的直线,存在以下
内的直线,存在以下三种情况:
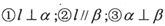 .若以其中两个为条件,另一个为结论,构成命题,
.若以其中两个为条件,另一个为结论,构成命题,其中正确命题的个数为
| A.0 | B.1 | C.2 | D.3 |
C
分析:分别利用线面垂直的性质及面面垂直的判定、面面垂直的性质及线面平行的判定,即可得到结论.
解:∵α、β表示平面,l表示不在α内也不在β内的直线,①l⊥α,②l∥β,③α⊥β,
∴以①②作为条件,③作为结论,即若l⊥α,l∥β,根据线面垂直的性质及面面垂直的判定,可得α⊥β,故是真命题;
以①③作为条件,②作为结论,即若l⊥α,α⊥β,根据面面垂直的性质及线面平行的判定,可得l∥β,故是真命题;
以②③作为条件,①作为结论,即若l∥β,α⊥β,则l⊥α,或l与α相交,故是假命题.
故选C.

练习册系列答案
相关题目
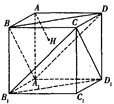
 的正方形,ABEF是矩形,且二面角C
的正方形,ABEF是矩形,且二面角C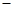 AB
AB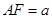 ,G是EF的中点,
,G是EF的中点,
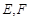 分别为BC,CD的中点,
分别为BC,CD的中点,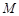 、
、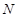 分别为AB、CF的中点,现沿AE、AF、EF折叠,使B、C、D三点重合,构成一个三棱锥
分别为AB、CF的中点,现沿AE、AF、EF折叠,使B、C、D三点重合,构成一个三棱锥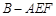 ,如图所示.
,如图所示.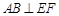 ;
;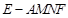 的体积.
的体积.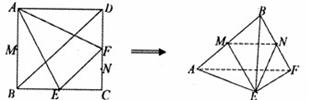
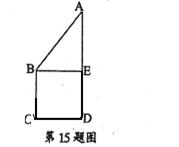
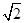 BC,将直角△ABE沿BE边折起,A点在面BCDE上的射影为D点,则翻折后的几何体中有如下描述:
BC,将直角△ABE沿BE边折起,A点在面BCDE上的射影为D点,则翻折后的几何体中有如下描述: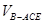 的体积是
的体积是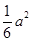 ;
;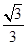 。
。
 ,则异面直线AD与BC所成角的大小为 .
,则异面直线AD与BC所成角的大小为 .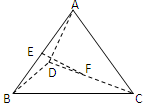
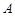 作平面
作平面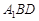 的垂线,垂足为
的垂线,垂足为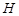 ,则以下命题中,错误的命题是
,则以下命题中,错误的命题是 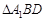 的垂心; ②
的垂心; ②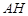 垂直平面
垂直平面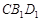 ;
;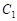 ; ④直线
; ④直线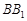 所成的角为
所成的角为