题目内容
【题目】设二次函数y=f(x)的最小值为4,且f(0)=f(2)=6,求f(x)的解析式.
【答案】解:∵二次函数y=f(x)满足f(0)=f(2),
∴二次函数y=f(x)图象的对称轴为 ![]() .
.
又∵二次函数y=f(x)的最小值为4,
∴二次函数y=f(x)图象的顶点坐标为(1,4),开口向上.
∴可设二次函数y=f(x)的解析式为f(x)=a(x﹣1)2+4(a>0).
∵f(0)=6,
∴a=2.
∴f(x)的解析式为f(x)=2x2﹣4x+6
【解析】本题可以根据条件找出抛物线的顶点,利用顶点式设出二次函数的解析式,再用一个点坐标代入,得到二次函数的解析式.
【考点精析】认真审题,首先需要了解二次函数的性质(当![]() 时,抛物线开口向上,函数在
时,抛物线开口向上,函数在![]() 上递减,在
上递减,在![]() 上递增;当
上递增;当![]() 时,抛物线开口向下,函数在
时,抛物线开口向下,函数在![]() 上递增,在
上递增,在![]() 上递减).
上递减).

练习册系列答案
相关题目
【题目】某工科院校对![]() ,
, ![]() 两个专业的男女生人数进行调查,得到如下的列联表:
两个专业的男女生人数进行调查,得到如下的列联表:
专业 | 专业 | 总计 | |
女生 | 12 | 4 | 16 |
男生 | 38 | 46 | 84 |
总计 | 50 | 50 | 100 |
(Ⅰ)从![]() 专业的女生中随机抽取2名女生参加某项活动,其中女生甲被选到的概率是多少?
专业的女生中随机抽取2名女生参加某项活动,其中女生甲被选到的概率是多少?
(Ⅱ)能否有95%的把握认为工科院校中“性别”与“专业”有关系?
附: 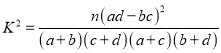 .
.
|
|
|
|
|
|
|
|
|
|
|
|