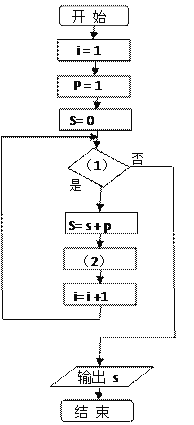
题目内容
【题目】设集合A=[0，
），B=[ ， 1]，函数f （x）=
， 若x0∈A，且f[f （x0）]∈A，则x0的取值范围是（ ）
A.（0，
]
B.[ ， ]
C.（ ， ）
D.[0，
]
【答案】C
【解析】解：∵0≤x0＜
， ∴f（x0）=x0 +∈[ ， 1]B，
∴f[f（x0）]=2（1﹣f（x0））=2[1﹣（x0+）]=2（﹣x0）．
∵f[f（x0）]∈A，∴0≤2（﹣x0）＜ ， ∴
＜x0≤ ．
又∵0≤x0＜ ， ∴＜x0＜ ．
故选C．
【考点精析】掌握元素与集合关系的判断和函数的值是解答本题的根本，需要知道对象
与集合
的关系是
，或者
，两者必居其一；函数值的求法：①配方法(二次或四次)；②“判别式法”；③反函数法；④换元法；⑤不等式法；⑥函数的单调性法．
练习册系列答案
高效智能课时作业系列答案
相关题目
