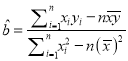题目内容
【题目】已知函数![]() ,且
,且![]() .
.
(Ⅰ)求函数![]() 的解析式;
的解析式;
(Ⅱ)若对任意![]() ,都有
,都有![]() ,求
,求![]() 的取值范围;
的取值范围;
(Ⅲ)证明函数![]() 的图象在
的图象在![]() 图象的下方.
图象的下方.
【答案】(Ⅰ)![]() ;(Ⅱ)
;(Ⅱ)![]() ;(Ⅲ)见解析.
;(Ⅲ)见解析.
【解析】试题分析:(Ⅰ)求函数![]() 的导数得
的导数得![]() ,由
,由![]() 求出
求出![]() 的值即可得到函数的解析式;(Ⅱ)
的值即可得到函数的解析式;(Ⅱ)![]() ,构造函数
,构造函数![]() ,则
,则![]() ,求函数
,求函数![]() 导数,利用导数求函数
导数,利用导数求函数![]() 即可;(Ⅲ)“函数
即可;(Ⅲ)“函数![]() 的图象在
的图象在![]() 图象的下方”等价于“
图象的下方”等价于“![]() 恒成立”
恒成立”![]() ,由(Ⅱ)可得
,由(Ⅱ)可得![]() 即
即![]() ,所以只要证
,所以只要证![]() 即
即![]() ,构造函数
,构造函数![]() ,证明在区间
,证明在区间![]() 上,
上,![]() 即可.
即可.
试题解析: (Ⅰ)易知![]() ,所以
,所以![]() ,又
,又![]() ………………1分
………………1分
∴![]() ……………………………2分
……………………………2分
∴![]() .…………………………3分
.…………………………3分
(Ⅱ)若对任意的![]() ,都有
,都有![]() ,
,
即![]() 恒成立,即:
恒成立,即:![]() 恒成立………………4分
恒成立………………4分
令![]() ,则
,则![]() ,…………………………6分
,…………………………6分
当![]() 时,
时,![]() ,所以
,所以![]() 单调递增;
单调递增;
当![]() 时,
时,![]() ,所以
,所以![]() 单调递减;……………………8分
单调递减;……………………8分
∴![]() 时,
时,![]() 有最大值
有最大值![]() ,
,
∴![]() ,即
,即![]() 的取值范围为
的取值范围为![]() .…………………………10分
.…………………………10分
(Ⅲ)要证明函数![]() 的图象在
的图象在![]() 图象的下方,
图象的下方,
即证:![]() 恒成立,
恒成立,
即:![]() ………………………11分
………………………11分
由(Ⅱ)可得:![]() ,所以
,所以![]() ,
,
要证明![]() ,只要证明
,只要证明![]() ,即证:
,即证:![]() ………………12分
………………12分
令![]() ,则
,则![]() ,
,
当![]() 时,
时,![]() ,所以
,所以![]() 单调递增,
单调递增,
∴![]() ,
,
即![]() ,……………13分
,……………13分
所以![]() ,从而得到
,从而得到![]() ,
,
所以函数![]() 的图象在
的图象在![]() 图象的下方.…………14分
图象的下方.…………14分

练习册系列答案
相关题目