题目内容
【题目】已知点（x，y）是区域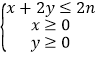
， （n∈N*）内的点，目标函数z=x+y，z的最大值记作zn ． 若数列{an}的前n项和为Sn ， a1=1，且点（Sn ， an）在直线zn=x+y上．
证明：数列{an﹣2}为等比数列
【答案】解：∵目标函数对应直线l：z=x+y，
区域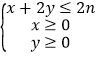
，（n∈N*）表示以x轴、y轴和直线x+2y=2n为三边的三角形，
∴当x=2n，y=0时，z的最大值zn=2n
∵（Sn ， an）在直线zn=x+y上
∴zn=Sn+an ， 可得Sn=2n﹣an ，
当n≥2时，可得an=Sn﹣Sn﹣1=（2n﹣an）﹣[2（n﹣1）﹣an﹣1]
化简整理，得2an=an﹣1+2
因此，an﹣2=
（an﹣1+2）﹣2=（an﹣1﹣2）
当n=1时，an﹣2=a1﹣2=﹣1
∴数列{an﹣2}是以﹣1为首项，公比q=的等比数列；
【解析】根据线性规划原理，可得z的最大值zn=2n，从而得到Sn=2n﹣an ． 运用数列前n项和Sn与an的关系，算出2an=an﹣1+2，由此代入数列{an﹣2}再化简整理，即可得到{an﹣2}是以﹣1为首项，公比q=的等比数列；
【考点精析】解答此题的关键在于理解等比关系的确定的相关知识，掌握等比数列可以通过定义法、中项法、通项公式法、前n项和法进行判断．
【题目】某班级举行一次知识竞赛活动，活动分为初赛和决赛两个阶段。现将初赛答卷成绩（得分均为整数，满分为100分）进行统计，制成如下频率分布表．
分数（分数段） | 频数（人数） | 频率 |
[60，70） | ① | 0.16 |
[70，80） | 22 | ② |
[80，90） | 14 | 0.28 |
[90，100] | ③ | ④ |
合 计 | 50 | 1 |
（1）填充频率分布表中的空格（在解答中直接写出对应空格序号的答案）；
（2）决赛规则如下：参加决赛的每位同学依次口答4道小题，答对2道题就终止答题，并获得一等奖。如果前三道题都答错，就不再答第四题。某同学进入决赛，每道题答对的概率
的值恰好与频率分布表中不少于80分的频率的值相同．
①求该同学恰好答满4道题而获得一等奖的概率；
②记该同学决赛中答题个数为
，求的分布列及数学期望．