题目内容
13.已知命题p:函数y=x2-2x+a在区间(1,2)上有1个零点;命题q:函数y=x2+(2a-3)x+1与x轴交于不同的两点.如果p∧q是假命题,p∨q是真命题,求a的取值范围.分析 对于命题p,设y=f(x),知道该函数为二次函数,对称轴为x=1,从而有$\left\{\begin{array}{l}{f(1)<0}\\{f(2)>0}\end{array}\right.$,解该不等式组即可得到0<a<1;对于命题q,则有△>0,从而可解得$a>\frac{5}{2}$,或a$<\frac{1}{2}$.并且根据条件可知p真q假,或p假q真,求出这两种情况的a的取值范围再求并集即可.
解答 解:对于命题p,设y=f(x)=x2-2x+a;
该二次函数开口向上,对称轴为x=1;
∴$\left\{\begin{array}{l}{f(1)=-1+a<0}\\{f(2)=a>0}\end{array}\right.$,∴0<a<1;
对于命题q:函数y=x2+(2a-3)x+1与x轴交于不同的两点;
∴△=(2a-3)2-4>0,即4a2-12a+5>0;
解得$a>\frac{5}{2}$或$a<\frac{1}{2}$;
∵p∧q是假命题,p∨q是真命题,∴命题p,q一真一假;
①p真q假,则$\left\{\begin{array}{l}0<a<1\\ \frac{1}{2}≤a≤\frac{5}{2}\end{array}\right.$,所以$\frac{1}{2}≤a<1$;
②p假q真,则$\left\{\begin{array}{l}a≥1或a≤0\\ a<\frac{1}{2}或a>\frac{5}{2}\end{array}\right.$,所以$a>\frac{5}{2}$或a≤0;
∴实数a的取值范围是(-∞,0]∪[$\frac{1}{2}$,1)∪($\frac{5}{2}$,+∞).
点评 考查函数零点的概念,求二次函数的对称轴的公式,以及二次函数图象和x轴交点的个数和判别式△的关系,要熟悉二次函数的图象,清楚p∧q,p∨q真假和p,q真假的关系.

| A. | 120(4) | B. | 130(4) | C. | 200(4) | D. | 202(4) |
| A. | (0,0) | B. | (1,1) | C. | (-1,-1) | D. | (1,1)或(-1,-1) |
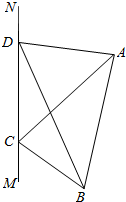 如图,为对某失事客轮AB进行有效援助,现分别在河岸MN选择两处C、D用强光柱进行辅助照明,其中A、B、C、D在同一平面内.现测得CD长为100米,∠ADN=105°,∠BDM=30°,∠ACN=45°,∠BCM=60°.
如图,为对某失事客轮AB进行有效援助,现分别在河岸MN选择两处C、D用强光柱进行辅助照明,其中A、B、C、D在同一平面内.现测得CD长为100米,∠ADN=105°,∠BDM=30°,∠ACN=45°,∠BCM=60°.