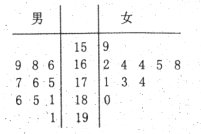
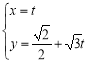题目内容
【题目】为了传承经典,促进学生课外阅读,某校从高中年级和初中年级各随机抽取100名学生进行有关对中国四大名著常识了解的竞赛.图1和图2分别是高中年级和初中年级参加竞赛的学生成绩按照![]() 分组,得到的频率分布直方图.
分组,得到的频率分布直方图.
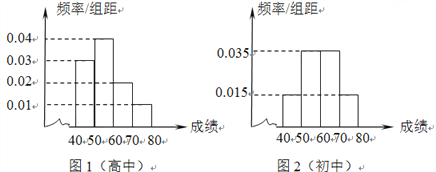
(1)分别计算参加这次知识竞赛的两个学段的学生的平均成绩;
(2)规定竞赛成绩达到![]() 为优秀,经统计初中年级有3名男同学,2名女同学达到优秀,现从上述5人中任选两人参加复试,求选中的2人恰好都为女生的概率;
为优秀,经统计初中年级有3名男同学,2名女同学达到优秀,现从上述5人中任选两人参加复试,求选中的2人恰好都为女生的概率;
(3)完成下列![]() 的列联表,并回答是否有99%的把握认为“两个学段的学生对四大名著的了解有差异”?
的列联表,并回答是否有99%的把握认为“两个学段的学生对四大名著的了解有差异”?
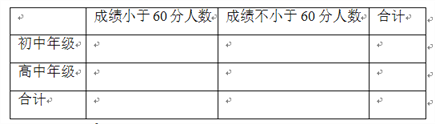
附: 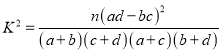
临界值表:
| 0.10 | 0.05 | 0.01 |
| 2.706 | 3.841 | 6.635 |
【答案】(1)![]() ;(2)
;(2)![]() ;(3)见解析.
;(3)见解析.
【解析】试题分析:
(1)由题意求得![]() ;
;
(2)由古典概型公式,选中的2人恰好都是女生的概率为![]() .
.
(3)由列联表求得![]() ,
,
故有99%的把握认为“两个学段的学生对四大名著的了解有差异”
试题解析:
(1)![]()
(2)从5名同学中任选2人参加复试的所有基本事件数有10个,其中选中的2人恰好都是女生的基本事件只有1个,故选中的2人恰好都是女生的概率为![]() .
.
(3)列联表如下
成绩小于60分人数 | 成绩不小于60分人数 | 合计 | |
初中年级 | 50 | 50 | 100 |
高中年级 | 70 | 30 | 100 |
合计 | 120 | 80 | 200 |
![]() ,
,
故有99%的把握认为“两个学段的学生对四大名著的了解有差异”

练习册系列答案
相关题目