题目内容
【题目】漳州市博物馆为了保护一件珍贵文物,需要在馆内一种透明又密封的长方体玻璃保护罩内充入保护液体.该博物馆需要支付的总费用由两部分组成:①罩内该种液体的体积比保护罩的容积少0.5立方米,且每立方米液体费用500元;②需支付一定的保险费用,且支付的保险费用与保护罩容积成反比,当容积为2立方米时,支付的保险费用为4000元.
(Ⅰ)求该博物馆支付总费用![]() 与保护罩容积
与保护罩容积![]() 之间的函数关系式;
之间的函数关系式;
(Ⅱ)求该博物馆支付总费用的最小值.
【答案】(Ⅰ)![]() (Ⅱ)博物馆支付总费用的最小值为3750元
(Ⅱ)博物馆支付总费用的最小值为3750元
【解析】【试题分析】(1)先依据题设分别求出支付的保险费用![]() 和保护液体的费用
和保护液体的费用![]() ,再求出运总费用
,再求出运总费用![]() 与保护罩容积
与保护罩容积![]() 之间的函数关系式
之间的函数关系式![]() ,(
,( ![]() );(2)依据题设条件运用基本不等式求出
);(2)依据题设条件运用基本不等式求出![]() 的最小值,从而确定函数
的最小值,从而确定函数![]() 的最小值:
的最小值:
解:(Ⅰ)由题意设支付的保险费用![]() ,把
,把![]() ,
, ![]() 代入,得
代入,得![]() .
.
则有支付的保险费用![]() (
(![]() )
)
故总费用![]() ,(
,( ![]() )
)
(Ⅱ)因为![]()
![]()
当且仅当![]() 且
且![]() ,
,
即![]() 立方米时不等式取等号,
立方米时不等式取等号,
所以,博物馆支付总费用的最小值为3750元.

练习册系列答案
相关题目
【题目】某种产品的年销售量![]() 与该年广告费用支出
与该年广告费用支出![]() 有关,现收集了4组观测数据列于下表:
有关,现收集了4组观测数据列于下表:
| 1 | 4 | 5 | 6 |
| 30 | 40 | 60 | 50 |
现确定以广告费用支出![]() 为解释变量,销售量
为解释变量,销售量![]() 为预报变量对这两个变量进行统计分析.
为预报变量对这两个变量进行统计分析.
(1)已知这两个变量满足线性相关关系,试建立![]() 与
与![]() 之间的回归方程;
之间的回归方程;
(2)假如2017年广告费用支出为10万元,请根据你得到的模型,预测该年的销售量![]() .
.
(线性回归方程系数公式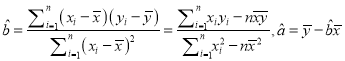 ).
).