题目内容
【题目】如图, ![]() 平面
平面![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 为
为![]() 的中点.
的中点.

(Ⅰ)证明: ![]() 平面
平面![]() ;
;
(Ⅱ)求多面体![]() 的体积;
的体积;
(Ⅲ)求二面角![]() 的正切值.
的正切值.
【答案】(Ⅰ)证明见解析(Ⅱ)![]() (Ⅲ)
(Ⅲ)![]()
【解析】【试题分析】(Ⅰ)先运用线面垂直的性质定理证明![]() ,再运用等腰三角形的性质证明
,再运用等腰三角形的性质证明![]() ,进而运用线面垂直的判定定理证明
,进而运用线面垂直的判定定理证明![]() 平面
平面![]() ;(Ⅱ)先求三棱锥的高
;(Ⅱ)先求三棱锥的高![]() 和底面三角形
和底面三角形![]() 面积
面积![]() ,用三棱锥的体积公式求出体积;(Ⅲ)先运用二面角平面角的定义找出二面角
,用三棱锥的体积公式求出体积;(Ⅲ)先运用二面角平面角的定义找出二面角![]() 的平面角
的平面角![]() ,再构造直角三角形
,再构造直角三角形![]() ,运用相似三角形的性质求出
,运用相似三角形的性质求出![]() ,最后运用解直角三角形的正切函数的定义求出
,最后运用解直角三角形的正切函数的定义求出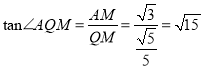 :
:
(Ⅰ)证明:∵![]() 平面
平面![]() ,
, ![]()
∴![]() 平面
平面![]()
∴![]() ①
①
又∵![]() ,点
,点![]() 为
为![]() 边中点
边中点
∴![]() ②
②
![]()
故由①②得![]() 平面
平面![]()
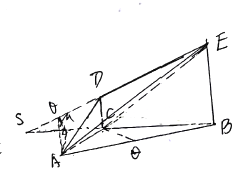
(Ⅱ)过点![]() 作
作![]() 交
交![]() 延长线于点
延长线于点![]()
∵![]()
∴![]() 平面
平面![]()
∴![]()
![]() ,
, ![]()
∴![]()
(Ⅲ)延长![]() 交
交![]() 延长线于
延长线于![]() ,过点
,过点![]() 作
作![]() 于
于![]() ,连结
,连结![]()
由(Ⅱ)可得: ![]() 为
为![]() 的平面角
的平面角
∵![]()
∴![]()
∴![]()
![]()
∵![]() ∽
∽![]()
∴![]()
∴![]() 即
即![]()
∴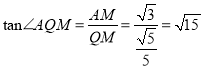

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目