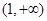题目内容
定义在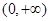 上的可导函数
上的可导函数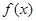 满足:
满足: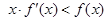 且
且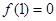 ,则
,则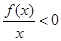 的解集为( )
的解集为( )
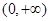 上的可导函数
上的可导函数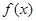 满足:
满足: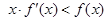 且
且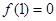 ,则
,则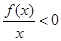 的解集为( )
的解集为( )A.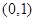 | B.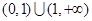 | C.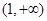 | D.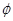 |
C
试题分析:令
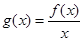 ,则
,则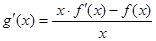 ,∵
,∵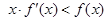 ,∴
,∴ ,∴g(x)在
,∴g(x)在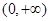 上单调递减,又
上单调递减,又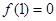 ,故g(1)=0,故
,故g(1)=0,故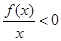 等价于g(x)<g(1), ∴x>1,∴
等价于g(x)<g(1), ∴x>1,∴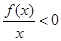 的解集为
的解集为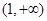
点评:构造函数利用导数法研究函数的单调性取求不等式的解集是解决此类问题的关键

练习册系列答案
相关题目
题目内容
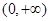 上的可导函数
上的可导函数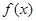 满足:
满足: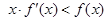 且
且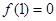 ,则
,则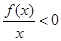 的解集为( )
的解集为( )A.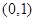 | B.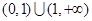 | C.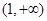 | D.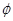 |
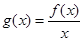 ,则
,则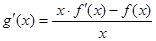 ,∵
,∵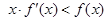 ,∴
,∴ ,∴g(x)在
,∴g(x)在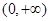 上单调递减,又
上单调递减,又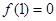 ,故g(1)=0,故
,故g(1)=0,故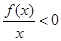 等价于g(x)<g(1), ∴x>1,∴
等价于g(x)<g(1), ∴x>1,∴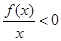 的解集为
的解集为