题目内容
函数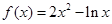 在其定义域的一个子区间
在其定义域的一个子区间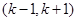 内部是单调函数,则实数
内部是单调函数,则实数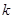 的取值范围是 ( )
的取值范围是 ( )
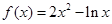 在其定义域的一个子区间
在其定义域的一个子区间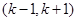 内部是单调函数,则实数
内部是单调函数,则实数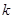 的取值范围是 ( )
的取值范围是 ( )A.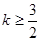 | B.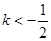 |
C.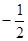 < <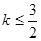 | D.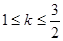 |
A
试题分析:求导函数,f′(x)=4x-
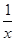 ,当k=1时,(k-1,k+1)为(0,2),函数在(0,
,当k=1时,(k-1,k+1)为(0,2),函数在(0,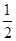 )上单调减,在(
)上单调减,在(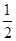 ,2)上单调增,满足题意;当k≠1时,∵函数f(x)=2x2-lnx在其定义域的一个子区间(k-1,k+1)内不是单调函数
,2)上单调增,满足题意;当k≠1时,∵函数f(x)=2x2-lnx在其定义域的一个子区间(k-1,k+1)内不是单调函数∴f′(x)在其定义域的一个子区间(k-1,k+1)内有正也有负
∴f′(k-1)f′(k+1)<0
∴(4k-4-
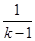 )(4k+4-
)(4k+4-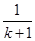 )<0
)<0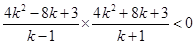 ∴
∴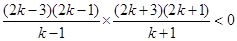
∵k-1>0∴k+1>0,,2k+1>0,2k+3>0,
∴(2k-3)(2k-1)><0,解得1<k<
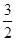 综上知,1≤k<
综上知,1≤k<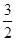 ,故可知如果内部有单调性,则可知
,故可知如果内部有单调性,则可知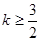 ,故选A.
,故选A.点评:解决该试题的关键是分类讨论,等价转化.利用反面的结论先期间诶内部不是单调函数,进而得到内部是单调函数的参数范围,

练习册系列答案
 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案
相关题目
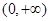 上的可导函数
上的可导函数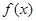 满足:
满足: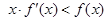 且
且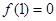 ,则
,则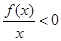 的解集为( )
的解集为( )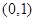
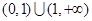
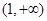
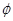
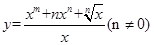
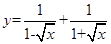
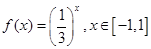 ,函数
,函数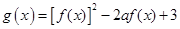 的最小值为
的最小值为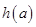 ,
,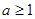 时,求
时,求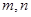 同时满足下列条件:①
同时满足下列条件:①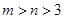 ;②当
;②当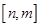 时,值域为
时,值域为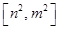
 ?若存在,求出
?若存在,求出 .
.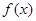 在
在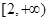 上是增函数,求实数
上是增函数,求实数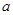 的取值范围;
的取值范围;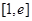 上的最小值为3,求实数
上的最小值为3,求实数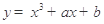 相切于点A(1,3)则b的值为
相切于点A(1,3)则b的值为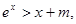 恒成立,则m的取值范围是 。
恒成立,则m的取值范围是 。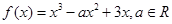
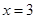 是
是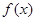 的极值点,求
的极值点,求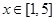 上的最大值
上的最大值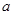 的取值范围.
的取值范围. 的切线
的切线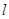 过点
过点 ,则切线
,则切线