题目内容
16.已知向量$\overrightarrow{a}$,$\overrightarrow{b}$,$\overrightarrow{c}$,满足|$\overrightarrow{a}$|=|$\overrightarrow{b}$|=|$\overrightarrow{a}$-$\overrightarrow{b}$|=|$\overrightarrow{a}$+$\overrightarrow{b}$-$\overrightarrow{c}$|=1,记|$\overrightarrow{c}$|的最大值为M,最小值为m,则M+m=( )| A. | 2$\sqrt{3}$ | B. | 2 | C. | $\sqrt{3}$ | D. | 1 |
分析 根据|$\overrightarrow{a}$|=|$\overrightarrow{b}$|=|$\overrightarrow{a}$-$\overrightarrow{b}$|=|$\overrightarrow{a}$+$\overrightarrow{b}$-$\overrightarrow{c}$|=1的几何意义可知,设$\overrightarrow{AB}=\overrightarrow{a}$,$\overrightarrow{AC}=\overrightarrow{b}$,则△ABC是等边三角形,得到$\overrightarrow{a}+\overrightarrow{b}=\overrightarrow{AD}$,得到C在以D为圆心的单位圆上,得到|$\overrightarrow{c}$|的最大值,最小值.
解答 解:由题意,设$\overrightarrow{AB}=\overrightarrow{a}$,$\overrightarrow{AC}=\overrightarrow{b}$,因为|$\overrightarrow{a}$|=|$\overrightarrow{b}$|=|$\overrightarrow{a}$-$\overrightarrow{b}$|=|$\overrightarrow{a}$+$\overrightarrow{b}$-$\overrightarrow{c}$|=1,则△ABC是等边三角形,
设$\overrightarrow{a}+\overrightarrow{b}=\overrightarrow{AD}$,$\overrightarrow{c}=\overrightarrow{AE}$,则E在以D为圆心的单位圆上,如图
所以|$\overrightarrow{c}$|的最大值为M=$\sqrt{3}+1$,最小值为m=$\sqrt{3}-1$,则M+m=2$\sqrt{3}$;
故选:A.
点评 本题考查了平面向量的几何意义的运用;关键是由已知的等式得到向量的位置关系.

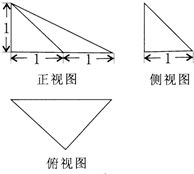
| A. | $\frac{\sqrt{6}}{2}$ | B. | $\frac{\sqrt{2}}{2}$ | C. | 1 | D. | $\frac{\sqrt{6}}{4}$ |
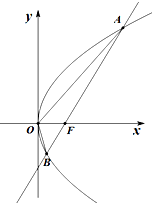 设抛物线C:y2=2px(p>0)的焦点为F,过F且斜率为k的直线l交抛物线C于A(x1,y1)、B(x2,y2)两点,且y1y2=-4.
设抛物线C:y2=2px(p>0)的焦点为F,过F且斜率为k的直线l交抛物线C于A(x1,y1)、B(x2,y2)两点,且y1y2=-4.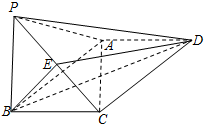 如图,在四棱锥P-ABCD中,底面ABCD为矩形,平面PAB⊥平面ABCD,PA⊥PB,BP=BC,E为PC的中点.
如图,在四棱锥P-ABCD中,底面ABCD为矩形,平面PAB⊥平面ABCD,PA⊥PB,BP=BC,E为PC的中点.