题目内容
8.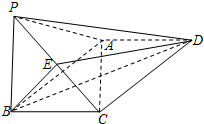 如图,在四棱锥P-ABCD中,底面ABCD为矩形,平面PAB⊥平面ABCD,PA⊥PB,BP=BC,E为PC的中点.
如图,在四棱锥P-ABCD中,底面ABCD为矩形,平面PAB⊥平面ABCD,PA⊥PB,BP=BC,E为PC的中点.(Ⅰ)求证:PA∥平面BDE;
(Ⅱ)求证:BE⊥平面PAC;
(Ⅲ)若AB=2BC,求二面角A-BC-E的大小.
分析 (Ⅰ)设AC∩BD=O,连接OE.证明OE∥PA,利用直线与平面平行的判定定理证明PA∥平面BDE.
(Ⅱ)通过证明BC⊥平面PAB,然后证明PA⊥BE.BE⊥PC留言在线与平面垂直的判定定理证明∴BE⊥平面PAC.(Ⅲ)说明∠ABP即为二面角A-BC-E的平面角,通过求解三角形即可得到二面角的大小.
解答 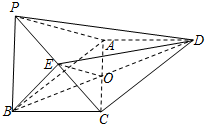 (本题13分)(文科)
(本题13分)(文科)
(Ⅰ)证明:设AC∩BD=O,连接OE.…(1 分)
∵底面ABCD为矩形,
∴O为AC的中点.
∵E为PC的中点,
∴OE∥PA.…(3 分)
∵PA?平面BDE,OE?平面BDE,
∴PA∥平面BDE.…(4 分)
(Ⅱ)证明:∵平面PAB⊥平面ABCD,BC⊥AB,
平面PAB∩平面ABCD=AB,BC?平面ABCD,
∴BC⊥平面PAB.…(5 分)
∵PA?平面PAB,
∴BC⊥PA.…(6 分)
∵PA⊥PB,BC∩PB=B,
∴PA⊥平面PBC.…(7 分)
∵BE?平面PBC,
∴PA⊥BE.…(8 分)
∵BP=BC,E为PC的中点,
∴BE⊥PC.…(9 分)
∵PA∩PC=P,
∴BE⊥平面PAC.…(10分)
(Ⅲ)解:由(Ⅱ)可知BC⊥平面PAB,
故∠ABP即为二面角A-BC-E的平面角.…(11分)
∵在Rt△APB中,∠APB=90°,AB=2BC=2BP,
∴∠BAP=30°,∠ABP=60°.
∴二面角A-BC-E为60°.…(13分)
点评 本题考查二面角的平面角的求法,直线与平面平行与垂直的判定定理的应用,考查空间想象能力逻辑推理能力,以及计算能力.

练习册系列答案
相关题目
16.已知向量$\overrightarrow{a}$,$\overrightarrow{b}$,$\overrightarrow{c}$,满足|$\overrightarrow{a}$|=|$\overrightarrow{b}$|=|$\overrightarrow{a}$-$\overrightarrow{b}$|=|$\overrightarrow{a}$+$\overrightarrow{b}$-$\overrightarrow{c}$|=1,记|$\overrightarrow{c}$|的最大值为M,最小值为m,则M+m=( )
| A. | 2$\sqrt{3}$ | B. | 2 | C. | $\sqrt{3}$ | D. | 1 |
3.已知实数ai,bi(i=1,2,3)满足a1<a2<a3,b1<b2<b3,且(ai-b1)(ai-b2)(ai-b3)=-1(i=1,2,3),则下列结论正确的是( )
| A. | b1<a1<a2<b2<b3<a3 | B. | a1<b1<b2<a2<a3<b3 | ||
| C. | a1<a2<b1<b2<a3<b3 | D. | b1<b2<a1<a2<b3<a3 |
17.如图,在正方体ABCD-A1B1C1D1中,下面结论不正确的是( )
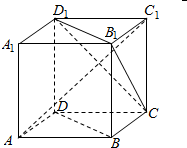

| A. | BD∥平面CB1D1 | B. | AC1⊥BD | ||
| C. | 平面ACC1A1⊥CB1D1 | D. | 异面直线AD与CB1所成的角为60° |
 如图,△BCD与△ECD都是边长为2的正三角形,平面ECD⊥平面BCD,AB⊥平面BCD,AB=2$\sqrt{3}$.
如图,△BCD与△ECD都是边长为2的正三角形,平面ECD⊥平面BCD,AB⊥平面BCD,AB=2$\sqrt{3}$.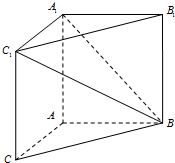 如图,在三棱柱ABC-A1B1C1中,AB=3,AA1=AC=4,AA1⊥平面ABC; AB⊥AC,
如图,在三棱柱ABC-A1B1C1中,AB=3,AA1=AC=4,AA1⊥平面ABC; AB⊥AC,