题目内容
1.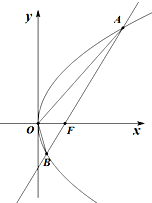 设抛物线C:y2=2px(p>0)的焦点为F,过F且斜率为k的直线l交抛物线C于A(x1,y1)、B(x2,y2)两点,且y1y2=-4.
设抛物线C:y2=2px(p>0)的焦点为F,过F且斜率为k的直线l交抛物线C于A(x1,y1)、B(x2,y2)两点,且y1y2=-4.(Ⅰ)求抛物线C的标准方程;
(Ⅱ)若k=1,O为坐标原点,求△OAB的面积.
分析 (Ⅰ)设直线AB的方程为y=k(x-$\frac{p}{2}$),代入抛物线,消x,利用y1y2=-4,求出p,即可求抛物线C的标准方程;
(Ⅱ)S△OAB=$\frac{1}{2}$×1×|y1-y2|,求△OAB的面积.
解答 解:(Ⅰ)F($\frac{p}{2}$,0),设直线AB的方程为y=k(x-$\frac{p}{2}$),…(2分)
代入抛物线,消x,得:ky2-2py-kp2=0,…(4分)
∴y1y2=-p2=-4,从而p=2,
∴抛物线C的方程为y2=4x. …(6分)
(Ⅱ)由已知,F(1,0),直线AB的方程为y=x-1,
代入抛物线,消x,得:y2-4y-4=0,
∴S△OAB=$\frac{1}{2}$×1×|y1-y2|=$\frac{1}{2}\sqrt{16+16}$=2$\sqrt{2}$…(15分)
点评 本题考查直线与抛物线的位置关系,考查三角形面积的计算,属于中档题.

练习册系列答案
 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案 学习实践园地系列答案
学习实践园地系列答案
相关题目
11.已知随机变量ξ服从正态分布N(2,1),若P(ξ>3)=0.023,则P(1≤ξ≤3)=( )
| A. | 0.046 | B. | 0.623 | C. | 0.977 | D. | 0.954 |
16.已知向量$\overrightarrow{a}$,$\overrightarrow{b}$,$\overrightarrow{c}$,满足|$\overrightarrow{a}$|=|$\overrightarrow{b}$|=|$\overrightarrow{a}$-$\overrightarrow{b}$|=|$\overrightarrow{a}$+$\overrightarrow{b}$-$\overrightarrow{c}$|=1,记|$\overrightarrow{c}$|的最大值为M,最小值为m,则M+m=( )
| A. | 2$\sqrt{3}$ | B. | 2 | C. | $\sqrt{3}$ | D. | 1 |
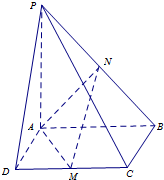 如图4,已知四棱锥P-ABCD,底面ABCD是正方形,PA⊥面ABCD,点M是CD的中点,点N是PB的中点,连接AM,AN,MN.
如图4,已知四棱锥P-ABCD,底面ABCD是正方形,PA⊥面ABCD,点M是CD的中点,点N是PB的中点,连接AM,AN,MN.