题目内容
4.已知映射f:P(m,n)→P′($\sqrt{m}$,$\sqrt{n}$)(m≥0,n≥0).设点A(2,6),B(4,4),点M是线段AB上一动点,f:M→M′.当点M是线段AB的中点时,点M′的坐标是($\sqrt{3}$,$\sqrt{5}$);当点M在线段AB上从点A开始运动到点B结束时,点M的对应点M′所经过的路线长度为$\frac{π}{3}$.分析 (1)由中点坐标公式得到M(3,5),由已知得到点M′的坐标是($\sqrt{3}$,$\sqrt{5}$).
(2)求点M′的轨迹方程,根据范围确定路径的长度.
解答 解:(1)∵点M是线段AB的中点,由中点坐标公式,
∴M(3,5),由已知映射f:P(m,n)→P′($\sqrt{m}$,$\sqrt{n}$)(m≥0,n≥0),
∴点M′的坐标是($\sqrt{3}$,$\sqrt{5}$).
(2)设M′(x,y),则M(x2,y2),线段AB方程为:x+y=8(2≤x≤4)
∴对应点M′为x2+y2=8($\sqrt{2}$≤x≤2,2≤y≤$\sqrt{6}$),
∴路径为一段圆弧,圆心角为15°,
∴点M的对应点M′所经过的路线长度为8π×$\frac{15}{360}$=$\frac{π}{3}$.
点评 主要考查轨迹问题,曲线与方程的运用,学生的灵活应用能力与计算能力.

练习册系列答案
相关题目
16.已知向量$\overrightarrow{a}$,$\overrightarrow{b}$,$\overrightarrow{c}$,满足|$\overrightarrow{a}$|=|$\overrightarrow{b}$|=|$\overrightarrow{a}$-$\overrightarrow{b}$|=|$\overrightarrow{a}$+$\overrightarrow{b}$-$\overrightarrow{c}$|=1,记|$\overrightarrow{c}$|的最大值为M,最小值为m,则M+m=( )
| A. | 2$\sqrt{3}$ | B. | 2 | C. | $\sqrt{3}$ | D. | 1 |
14.已知 (1-2i)z=5(i为虚数单位),则复数z在复平面内对应的点所在象限为( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
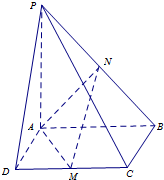 如图4,已知四棱锥P-ABCD,底面ABCD是正方形,PA⊥面ABCD,点M是CD的中点,点N是PB的中点,连接AM,AN,MN.
如图4,已知四棱锥P-ABCD,底面ABCD是正方形,PA⊥面ABCD,点M是CD的中点,点N是PB的中点,连接AM,AN,MN.