题目内容
5.(1)设函数f(x)=|x-1|+$\frac{1}{2}$|x-3|,求不等式f(x)<2的解集;(2)若a,b,c都为正实数,且满足a+b+c=2,证明:$\frac{1}{a}$+$\frac{1}{b}$+$\frac{1}{c}$≥$\frac{9}{2}$.
分析 (1)把要解的不等式等价转化为与之等价的三个不等式组,求出每个不等式组的解集,再取并集,即得所求.
(2)由条件把不等式的左边化为 $\frac{1}{2}$[3+$\frac{b}{a}+\frac{a}{b}$+$\frac{c}{b}+\frac{c}{b}$+$\frac{c}{a}$+$\frac{a}{c}$],再利用基本不等式证得结论.
解答 解:(1)根据f(x)=|x-1|+$\frac{1}{2}$|x-3|,由不等式f(x)<2,
可得 $\left\{\begin{array}{l}{x≤1}\\{1-x+\frac{1}{2}(3-x)<2}\end{array}\right.$ ①,或$\left\{\begin{array}{l}{1<x<3}\\{x-1+\frac{1}{2}(3-x)<2}\end{array}\right.$②,或$\left\{\begin{array}{l}{x≥3}\\{x-1+\frac{1}{2}(x-3)<2}\end{array}\right.$③.
解①求得 $\frac{1}{3}$<x≤1,解②求得1<x<3,解③求得 x∈∅,
综上可得,原不等式的解集为{x|<x<3}.
(2)∵a+b+c=2,∴$\frac{1}{a}$+$\frac{1}{b}$+$\frac{1}{c}$=$\frac{1}{2}$[$\frac{a+b+c}{a}$+$\frac{a+b+c}{b}$+$\frac{a+b+c}{c}$]=$\frac{1}{2}$[3+$\frac{b}{a}+\frac{c}{a}$+$\frac{a}{b}+\frac{c}{b}$+$\frac{a}{c}+\frac{b}{c}$]
=$\frac{1}{2}$[3+$\frac{b}{a}+\frac{a}{b}$+$\frac{c}{b}+\frac{c}{b}$+$\frac{c}{a}$+$\frac{a}{c}$]≥$\frac{1}{2}$(3+2+2+2)=$\frac{9}{2}$,
当且仅当a=b=c时,取等号,故$\frac{1}{a}$+$\frac{1}{b}$+$\frac{1}{c}$≥$\frac{9}{2}$成立.
点评 本题主要考查绝对值不等式的解法,用基本不等式证明不等式,体现了转化、分类讨论的数学思想,属于基础题.

 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案| A. | 2$\sqrt{3}$ | B. | 2 | C. | $\sqrt{3}$ | D. | 1 |
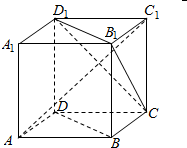
| A. | BD∥平面CB1D1 | B. | AC1⊥BD | ||
| C. | 平面ACC1A1⊥CB1D1 | D. | 异面直线AD与CB1所成的角为60° |
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
 如图,△BCD与△ECD都是边长为2的正三角形,平面ECD⊥平面BCD,AB⊥平面BCD,AB=2$\sqrt{3}$.
如图,△BCD与△ECD都是边长为2的正三角形,平面ECD⊥平面BCD,AB⊥平面BCD,AB=2$\sqrt{3}$.