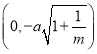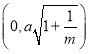题目内容
【题目】设函数![]() .
.
(1)若不等式![]() 解集为
解集为![]() ,求实数
,求实数![]() 的值;
的值;
(2)在(1)的条件下,若不等式![]() 解集非空,求实数
解集非空,求实数![]() 的取值范围.
的取值范围.
【答案】(1)-2;(2)![]() 或
或![]() 或
或![]() .
.
【解析】
(1)由题意把不等式化为|x﹣2a|≤2﹣a,去掉绝对值,写出x的取值范围,再根据不等式的解集列方程求出a的值;
(2)把不等式化为|x+4|+1≤(k2﹣1)x,设g(x)=|x+4|+1,作出g(x)的图象,结合图象知要使不等式的解集非空,应满足的条件是什么,由此求得k的取值范围.
解:(1)函数f(x)=![]() +a,
+a,
∴不等式f(x)≤2化为![]() ≤2﹣a,
≤2﹣a,
∴a﹣2≤x﹣2a≤2﹣a,
解得3a﹣2≤x≤a+2;
又f(x)≤2的解集为{x|﹣8≤x≤0},
∴![]() ,
,
解得a=﹣2;
(2)在(1)的条件下,f(x)=|x﹣4|﹣2,
不等式f(x)≤(k2﹣1)x﹣3化为|x+4|+1≤(k2﹣1)x,
令g(x)=|x+4|+1![]() ,作出g(x)的图象,如图所示;
,作出g(x)的图象,如图所示;

由图象知,要使不等式的解集非空,应满足:
k2﹣1>1或k2﹣1![]() ,
,
即k2>2或k2![]() ,
,
解得k![]() 或
或![]() k
k![]() 或x
或x![]() ,
,
所以实数k的取值范围是{k|k![]() 或
或![]() k
k![]() 或k
或k![]() }.
}.

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案
相关题目