题目内容
【题目】已知椭圆C:![]() 上的点到右焦点F的最大距离为
上的点到右焦点F的最大距离为![]() ,离心率为
,离心率为![]() .
.
![]() 求椭圆C的方程;
求椭圆C的方程;
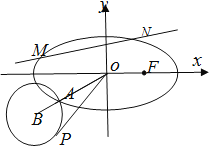
![]() 如图,过点
如图,过点![]() 的动直线l交椭圆C于M,N两点,直线l的斜率为
的动直线l交椭圆C于M,N两点,直线l的斜率为![]() ,A为椭圆上的一点,直线OA的斜率为
,A为椭圆上的一点,直线OA的斜率为![]() ,且
,且![]() ,B是线段OA延长线上一点,且
,B是线段OA延长线上一点,且![]() 过原点O作以B为圆心,以
过原点O作以B为圆心,以![]() 为半径的圆B的切线,切点为
为半径的圆B的切线,切点为![]() 令
令![]() ,求
,求![]() 取值范围.
取值范围.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】
![]() 依题
依题![]() ,结合离心率求得a与c的值,再由隐含条件求得b,则椭圆方程可求;
,结合离心率求得a与c的值,再由隐含条件求得b,则椭圆方程可求;
![]() 由已知可得直线l的方程,与椭圆C:
由已知可得直线l的方程,与椭圆C:![]() 联立,化为关于x的一元二次方程,利用弦长公式求得弦
联立,化为关于x的一元二次方程,利用弦长公式求得弦![]() ,写出OA所在直线方程,与椭C:
,写出OA所在直线方程,与椭C:![]() 联立求得
联立求得![]() ,得到
,得到![]() ,利用换元法求得
,利用换元法求得![]() 的范围,把
的范围,把![]() 转化为含
转化为含![]() 的代数式求解.
的代数式求解.
![]() 依题
依题![]() ,
,![]() ,
,
解得![]() ,
,![]() ,
,
![]() .
.
![]() 椭圆C的方程为
椭圆C的方程为![]() ;
;
![]() 由已知可得直线l的方程为:
由已知可得直线l的方程为:![]() ,与椭圆C:
,与椭圆C:![]() 联立,
联立,
得![]() ,由题意
,由题意![]() ,
,
设![]() ,
,![]() ,则
,则![]() ,
,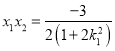 .
.
![]() 弦
弦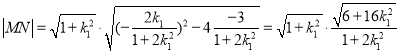 ,
,
OA所在直线方程为![]() ,与椭C:
,与椭C:![]() 联立,解得
联立,解得![]() ,
,
 .
.
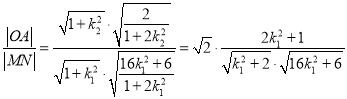 .
.
令![]() ,则
,则![]() ,
,
则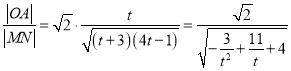 ,
,
得到 ,
,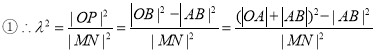
![]() .
.
令![]() ,由
,由![]() 知,
知,![]() ,换元得:
,换元得:
![]() ,其中
,其中![]() .
.
![]() .
.

练习册系列答案
相关题目