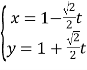题目内容
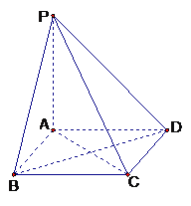
【题目】如图,在多面体![]() 中,
中,![]() 平面
平面![]() ,四边形
,四边形![]() 为正方形,四边形
为正方形,四边形![]() 为梯形,且
为梯形,且![]() ,
,![]() ,
,![]() ,
,![]() .
.
(1)求直线![]() 与平面
与平面![]() 所成角的正弦值;
所成角的正弦值;
(2)线段![]() 上是否存在点
上是否存在点![]() ,使得直线
,使得直线![]() 平面
平面![]() ?若存在,求
?若存在,求![]() 的值:若不存在,请说明理由.
的值:若不存在,请说明理由.
【答案】(1) ![]() ;(2)
;(2) ![]() .
.
【解析】
建立适当的空间直角坐标系.
(1)求出平面![]() 的法向量,利用空间向量夹角公式可以求出直线
的法向量,利用空间向量夹角公式可以求出直线![]() 与平面
与平面![]() 所成角的正弦值;
所成角的正弦值;
(2)求出平面![]() 的法向量,结合线面平行的性质,空间向量共线的性质,如果求出
的法向量,结合线面平行的性质,空间向量共线的性质,如果求出![]() 的值,也就证明出存在线段
的值,也就证明出存在线段![]() 上是否存在点
上是否存在点![]() ,使得直线
,使得直线![]() 平面
平面![]() ,反之就不存在.
,反之就不存在.
以![]() 为空间直角坐标系的原点, 向量
为空间直角坐标系的原点, 向量![]() 所在的直线为
所在的直线为![]() 轴.如下所示:
轴.如下所示:![]() .
.
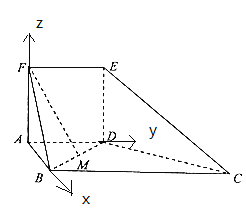
(1)平面![]() 的法向量为
的法向量为![]() ,
,![]() .
.
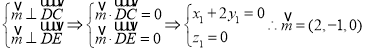 .
.
直线![]() 与平面
与平面![]() 所成角为
所成角为![]() ,所以有
,所以有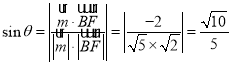 ;
;
(2)假设线段![]() 上是存在点
上是存在点![]() ,使得直线
,使得直线![]() 平面
平面![]() .设
.设![]() ,因此
,因此![]() ,所以
,所以![]() 的坐标为:
的坐标为:![]() .
.![]() .
.
设平面![]() 的法向量为
的法向量为![]() ,
,![]() ,
,
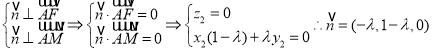 ,
,
因为直线![]() 平面
平面![]() ,所以有
,所以有![]() ,即
,即![]() .
.

练习册系列答案
相关题目
【题目】对某校高一年级学生参加社区服务次数进行统计,随机抽取M名学生作为样本,得到这M名学生参加社区服务的次数.根据此数据作出了频数与频率的统计表和频率分布直方图如下:
分组 | 频数 | 频率 |
[10,15) | 10 | 0.25 |
[15,20) | 25 | n |
[20,25) | m | p |
[25,30) | 2 | 0.05 |
合计 | M | 1 |
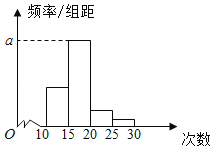
(1)求出表中M,p及图中a的值;
(2)若该校高一学生有360人,试估计该校高一学生参加社区服务的次数在区间[15,20)内的人数;
(3)在所取样本中,从参加社区服务的次数不少于20次的学生中任选2人,请列举出所有基本事件,并求至多1人参加社区服务次数在区间[20,25)内的概率.