题目内容

13．已知数列{an}满足a1=a2=1，an+2=an+1+an（n∈N•）．若存在正实数λ使得数列|an+1+λan|为等比数列，则λ=$\frac{-1+\sqrt{5}}{2}$．

分析 通过变形可得an+2+λan+1=（1+λ）（an+1+$\frac{1}{1+λ}$an），只需$\frac{1}{1+λ}$=λ，计算即得结论．

解答 解：由题意可知：an+2+λan+1=（1+λ）an+1+an=（1+λ）（an+1+$\frac{1}{1+λ}$an），
∴$\frac{1}{1+λ}$=λ，解得：λ=$\frac{-1+\sqrt{5}}{2}$或λ=$\frac{-1-\sqrt{5}}{2}$（舍），
∵a1=a2=1，∴a3=2，
易验证当n=1时满足题意，
故答案为：$\frac{-1+\sqrt{5}}{2}$．

点评 本题考查等比数列的概念，注意解题方法的积累，属于中档题．

练习册系列答案
相关题目
3．异面直线l与m成60°，异面直线l与n成45°，则异面直线m与n成角范围是（　　）
A．[15°，90°]B．[60°，90°]C．[15°，105°]D．[30°，105°]
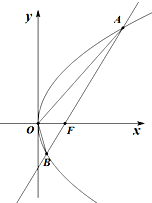4．已知映射f：P（m，n）→P′（$\sqrt{m}$，$\sqrt{n}$）（m≥0，n≥0）．设点A（2，6），B（4，4），点M是线段AB上一动点，f：M→M′．当点M是线段AB的中点时，点M′的坐标是（$\sqrt{3}$，$\sqrt{5}$）；当点M在线段AB上从点A开始运动到点B结束时，点M的对应点M′所经过的路线长度为$\frac{π}{3}$．
1．设抛物线C：y2=2px（p＞0）的焦点为F，过F且斜率为k的直线l交抛物线C于A（x1，y1）、B（x2，y2）两点，且y1y2=-4．
（Ⅰ）求抛物线C的标准方程；
（Ⅱ）若k=1，O为坐标原点，求△OAB的面积．
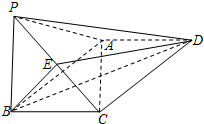8．如图，在四棱锥P-ABCD中，底面ABCD为矩形，平面PAB⊥平面ABCD，PA⊥PB，BP=BC，E为PC的中点．
（Ⅰ）求证：PA∥平面BDE；
（Ⅱ）求证：BE⊥平面PAC；
（Ⅲ）若AB=2BC，求二面角A-BC-E的大小．
18．在区间[-3，3]上随机取一个数x，使得$\frac{3-x}{x+1}$≥0成立的概率为$\frac{2}{3}$．
5．（1）设函数f（x）=|x-1|+$\frac{1}{2}$|x-3|，求不等式f（x）＜2的解集；
（2）若a，b，c都为正实数，且满足a+b+c=2，证明：$\frac{1}{a}$+$\frac{1}{b}$+$\frac{1}{c}$≥$\frac{9}{2}$．
2．设函数f（x）=sin（ωx+φ）（ω，φ是常数，ω＞0），若f（x）在区间[$\frac{1}{3}$，1]上具有单调性，且f（0）=f（$\frac{2}{3}$）=-f（1），则下列有关f（x）的命题正确的有①③④⑤（把所有正确的命题序号都写上）
①f（x）的最小正周期为2；
②f（x）在[1，$\frac{5}{3}$]上具有单调性；
③当x=$\frac{1}{3}$时，函数f（x）取得最值；
④y=f（x+$\frac{5}{6}$）为奇函数；
⑤（-$\frac{φ}{ω}$，-φ）是y=f（x）+ωx图象的一个对称中心．
3．已知等差数列{an}的前n项和为Sn=-n2+（10+k）n+（k-1），则实数k=1，an=-2n+12，Sn的最大值为30．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网