题目内容
12.在△ABC中,若a=2,b=2$\sqrt{3},B=\frac{π}{3}$,则△ABC的面积为$2\sqrt{3}$.分析 利用已知条件判断三角形的形状,直接求解三角形的面积.
解答 解:在△ABC中,若a=2,b=2$\sqrt{3},B=\frac{π}{3}$,
可得sinA=$\frac{asinB}{b}$=$\frac{1}{2}$,a<b,可得A=$\frac{π}{6}$,
三角形是直角三角形,
则△ABC的面积为:$\frac{1}{2}×2×2\sqrt{3}$=$2\sqrt{3}$.
故答案为:$2\sqrt{3}$.
点评 本题考查正弦定理的应用,三角形的解法,考查计算能力.

练习册系列答案
相关题目
2.复数z=1-i,则$\frac{1}{z}+{z^2}$对应的点所在象限为( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
3.异面直线l与m成60°,异面直线l与n成45°,则异面直线m与n成角范围是( )
| A. | [15°,90°] | B. | [60°,90°] | C. | [15°,105°] | D. | [30°,105°] |
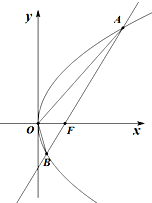 设抛物线C:y2=2px(p>0)的焦点为F,过F且斜率为k的直线l交抛物线C于A(x1,y1)、B(x2,y2)两点,且y1y2=-4.
设抛物线C:y2=2px(p>0)的焦点为F,过F且斜率为k的直线l交抛物线C于A(x1,y1)、B(x2,y2)两点,且y1y2=-4.