题目内容
10．若曲线f（x，y）=0上两个不同点处的切线重合，则称这条切线为曲线f（x，y）=0的“自公切线”．下列方程①x2-y2=1；②y=x2-|x|；③y=3sinx+4cosx；④|x|+1=$\sqrt{4-{y}^{2}}$；⑤$\frac{{x}^{2}}{16}$+$\frac{{y}^{2}}{9}$=1对应的曲线中存在“自公切线”的有②③．分析 ①x2-y2=1 是一个等轴双曲线，没有自公切线；
②在x=$\frac{1}{2}$和x=-$\frac{1}{2}$处的切线都是y=-$\frac{1}{4}$，故②有自公切线．
③此函数是周期函数，过图象的最高点的切线都重合或过图象的最低点的切线都重合，故此函数有自公切线．
④结合图象可得，此曲线没有自公切线．
⑤$\frac{{x}^{2}}{16}$+$\frac{{y}^{2}}{9}$=1，根据“自公切线”的定义，此曲线没有自公切线．
解答 解：①x2-y2=1 是一个等轴双曲线，没有自公切线；
②y=x2-|x|，在x=$\frac{1}{2}$和x=-$\frac{1}{2}$处的切线都是y=-$\frac{1}{4}$，故②有自公切线．
③y=3sinx+4cosx=5sin（x+φ），cosφ=$\frac{3}{5}$，sinφ=$\frac{4}{5}$，此函数是周期函数，过图象的最高点的切线都重合或过图象的最低点的切线都重合，故此函数有自公切线．
④由于|x|+1=$\sqrt{4-{y}^{2}}$，即 x2+2|x|+y2-3=0，结合图象可得，此曲线没有自公切线．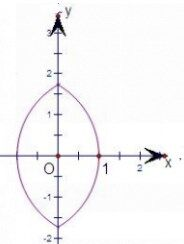
⑤$\frac{{x}^{2}}{16}$+$\frac{{y}^{2}}{9}$=1，根据“自公切线”的定义，此曲线没有自公切线．
故答案为：②③．
点评 正确理解新定义“自公切线”，正确画出函数的图象、数形结合的思想方法是解题的关键．
练习册系列答案
口算能手系列答案
相关题目
设抛物线C：y2=2px（p＞0）的焦点为F，过F且斜率为k的直线l交抛物线C于A（x1，y1）、B（x2，y2）两点，且y1y2=-4．
在四棱柱ABCD-A′B′C′D′中，底面ABCD为正方形，侧棱AA′⊥底面ABCD，AB=2，AA′=4．给出下面五个命题：
19．已知点A（-1.0），B（1，0），若圆 （x-2）2+y2=r2上存在点P．使得∠APB=90°，则实数r的取值范围为（ ）
| A． | （1，3） | B． | [1，3] | C． | （1，2] | D． | [2，3] |
如图已知椭圆G：$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）的左、右两个焦点分别为F1、F2，设A（0，b），若△AF1F2为正三角形且周长为6．