题目内容
11.已知an+1=2an+3(n∈N*),且a1=1,Sn为数列{an}的前n项和.(1)求数列{an}的通项公式;
(2)求S20.
分析 (1)将递推公式化为:an+1+3=2(an+3),利用等比数列的定义判断出数列{an+3}是等比数列,利用等比数列的通项公式求出an;
(2)由(1)求出的通项公式an,利用分组求和法和等比数列的前n项和公式求出S20.
解答 解:(1)由题意得,an+1=2an+3,则an+1+3=2(an+3),
所以$\frac{{a}_{n+1}+3}{{a}_{n}+3}=2$,
又a1=1,则a1+3=4,
所以数列{an+3}是以4为首项、2为公比的等比数列,
所以an+3=4•2n-1=2n+1,则an=2n+1-3;
(2)由(1)得,S20=(22-3)+(23-3)+…+(221-3)
=22+23+…+221-3×20
=$\frac{4(1-{2}^{20})}{1-2}$-60=222-64.
点评 本题考查了等比数列的定义、通项公式、前n项和公式,以及分组求和法、构造法的应用,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
19.已知点A(-1.0),B(1,0),若圆 (x-2)2+y2=r2上存在点P.使得∠APB=90°,则实数r的取值范围为( )
| A. | (1,3) | B. | [1,3] | C. | (1,2] | D. | [2,3] |
6.某三棱锥的三视图如图所示,则该三棱锥各面中,最小的面积为( )


| A. | $\frac{\sqrt{6}}{2}$ | B. | $\frac{\sqrt{2}}{2}$ | C. | 1 | D. | $\frac{\sqrt{6}}{4}$ |
4.在等比数列{an}中,a6与a7的等差中项等于48,a4a5a6a7a8a9a10=1286,如果设{an}的前n项和为Sn,那么Sn=( )
| A. | 5n-4 | B. | 4n-3 | C. | 3n-2 | D. | 2n-1 |
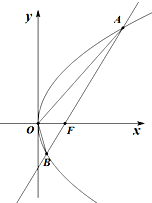 设抛物线C:y2=2px(p>0)的焦点为F,过F且斜率为k的直线l交抛物线C于A(x1,y1)、B(x2,y2)两点,且y1y2=-4.
设抛物线C:y2=2px(p>0)的焦点为F,过F且斜率为k的直线l交抛物线C于A(x1,y1)、B(x2,y2)两点,且y1y2=-4. 如图已知椭圆G:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左、右两个焦点分别为F1、F2,设A(0,b),若△AF1F2为正三角形且周长为6.
如图已知椭圆G:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左、右两个焦点分别为F1、F2,设A(0,b),若△AF1F2为正三角形且周长为6.