题目内容
【题目】直线
与椭圆
相交于
，
两点，该椭圆上点
使得
的面积等于
，这样的点共有（ ）
A.
个B.
个C.
个D.个
【答案】B
【解析】
联立直线与椭圆方程，得
、
，得
，结合
的面积等于
，可得
到
的距离为
为
，然后求出与已知直线平行，且与椭圆相切的直线
与
，算出两条直线中一条与椭圆有两个交点而另一条与椭圆无交点，由此即可得到使的面积等于的点个数，即可求得答案.
联立直线直线
与椭圆
，
得
或
，
直线与椭圆的交点为和，
可得
设点到的距离为，
则
，即
解之得
设平行于直线与椭圆相切的直线为
联立与椭圆
即：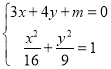
联立消去
可得：
可得
由此可得两条平行于直线的切线分别为：
和
与直线的距离
与直线的距离
与中，与椭圆相交，有两个交点，而与椭圆相离，没有交点.
有
个点使的面积等于，
故选：B.
精英口算卡系列答案
【题目】3月3日，武汉大学人民医院的团队在预印本平台
上发布了一项研究：在新冠肺炎病例的统计数据中，男性患者往往比女性患者多.研究者分析了1月1日~29日的6013份病例数据，发现
的患者为男性；进入重症监护病房的患者中，则有
为男性.随后，他们分析了武汉大学人民医院的数据.他们按照症状程度的不同进行分析，结果发现，男性患者有
为危重，而女性患者危重情况的为
.也就是说男性的发病情况似乎普遍更严重.研究者总结道：“男性在新冠肺炎的传播中扮演着重要的角色.”那么，病毒真的偏爱男性吗？有一个中学生学习小组，在自己封闭的社区进行无接触抽样问卷调查，收集到男、女患者各50个数据，统计如下：
轻—中度感染 | 重度（包括危重） | 总计 | |
男性患者 |
|
|
|
女性患者 |
|
|
|
总计 |
|
|
|
（1）求
列联表中的数据
的值；
（2）能否有
把握认为，新冠肺炎的感染程度和性别有关？
（3）该学生实验小组打算从“轻—中度感染”的患者中按男女比例再抽取5人，追踪某种中药制剂的效果.然后从这5人中随机抽取3人进行每日的健康记录，求至少抽到2名女性患者的概率.
附表及公式：
.
|
|
|
|
|
|
|
|
|
|
|
|
【题目】某市一调查机构针对该市市场占有率最高的甲、乙两家网络外卖企业以下简称外卖甲，外卖乙的经营情况进行了调查，调查结果如表：
日期 | 第1天 | 第2天 | 第3天 | 第4天 | 第5天 |
外卖甲日接单x(百单 | 5 | 2 | 9 | 8 | 11 |
外卖乙日接单y(百单 | 2.2 | 2.3 | 10 | 5 | 15 |
（Ⅰ）据统计表明，y与x之间具有线性相关关系．经计算求得y与x之间的回归方程为
，假定每单外卖业务企业平均能获纯利润3元，试预测当外卖乙日接单量不低于2500单时，外卖甲所获取的日纯利润的大致范围；(x值精确到0.01)
（Ⅱ）试根据表格中这五天的日接单量情况，从平均值和方差角度说明这两家外卖企业的经营状况．
