题目内容
【题目】如图,四棱锥![]() 中,平面
中,平面![]() 平面
平面![]() ,
,![]() 为线段
为线段![]() 上一点,
上一点,![]() ,
, ![]() 为
为![]() 的中点.
的中点.
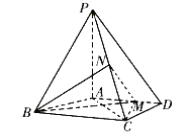
(1)证明:![]() 平面
平面![]() ;
;
(2)求三棱锥C-BMN的体积.
【答案】(1)见解析;(2)![]()
【解析】
(1)利用平面与平面平行判定,得到平面ENM平行平面PAB,结合平面与平面平行性质,即可。(2)将该三棱锥转化,利用余弦定理,并结合三角形面积计算公式,计算体积,即可。
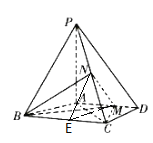
(1)取BC的中点为E,联结ME,NE,结合AD=3,且AM=2MD,可得MA=2,而BC=4,得到BE=2,结合AM平行BE,可得四边形ABEM为平行四边形, 结合性质,得到ME平行AB,而N为PC的中点,结合三角形中位线定理,得到NE平行PB,结合平面与平面平行判定,得到平面ENM平行平面PAB,而MN包含在平面ENM,结合性质,得到MN![]() 平面PAB。
平面PAB。
(2)对三角形ABC而言,AC=3,AB=3,CB=4,利用余弦定理,得到![]() ,结合
,结合![]()
得到![]() ,所以
,所以![]() ,结合平面PAB垂直平面ABCD,而
,结合平面PAB垂直平面ABCD,而![]() ,得到三角形PAB为直角三角形,得到PA垂直平面ABCD,该三棱锥高为
,得到三角形PAB为直角三角形,得到PA垂直平面ABCD,该三棱锥高为![]() 2,所以体积为
2,所以体积为![]()

 同步学典一课多练系列答案
同步学典一课多练系列答案 经典密卷系列答案
经典密卷系列答案 金牌课堂练系列答案
金牌课堂练系列答案 三新快车金牌周周练系列答案
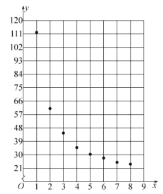
三新快车金牌周周练系列答案【题目】某企业新研发了一种产品,产品的成本由原料成本及非原料成本组成,每件产品的非原料成本y(元)与生产该产品的数量x(千件)有关,经统计得到如下数据:
x | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
y | 112 | 61 | 44.5 | 35 | 30.5 | 28 | 25 | 24 |
根据以上数据,绘制了散点图.
参考数据:(其中![]() )
)
|
|
|
|
|
|
183.4 | 0.34 | 0.115 | 1.53 | 360 | 22385.8 |
参考公式:对于一组数据![]() ,
,![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计分别为:
的斜率和截距的最小二乘估计分别为: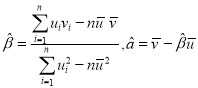 .
.
(1)观察散点图判断,![]() 与
与![]() 哪一个适宜作为非原料成本y与生产该产品的数量x的回归方程类型?(给出判断即可,不必说明理由)
哪一个适宜作为非原料成本y与生产该产品的数量x的回归方程类型?(给出判断即可,不必说明理由)
(2)根据(1)的判断结果及表中数据,建立y与x的回归方程.
(3)试预测生产该产品10000件时每件产品的非原料成本.
